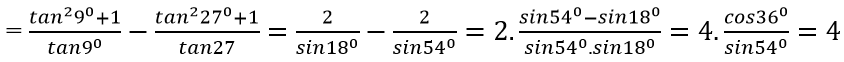Tính 4(cos24° + cos48° – cos84° – cos12°)

Ôn tập cuối năm

Bài 9 trang 161 Toán 10: Tính

a) 4(cos24° + cos48° – cos84° – cos12°)

b) 96√3 sin⁡(π/48) cos(⁡π/48) cos⁡(π/24) cos⁡(π/12) cos⁡(π/6)

c) tan9° – tan63° + tan81° – tan27°

Trả lời

a) 4(cos24° + cos48° – cos84° – cos12°)

= 4(2cos36°.cos12° – (2cos48° – cos36°)

= 4(2cos36° (cos12° – cos48°)

= 4(2cos36°(2sin30°.sin18°)

= 8cos360sin18° (cos36°sin18°) = 2

b) 96√3 sin ⁡π/48 cos ⁡ π/48 cos ⁡π/24 cos π/12 cos π/6

= 96√3.1/2.sin ⁡ π/24 cos ⁡ π/24 cos⁡π/12 cos⁡π/6

= 96√3.1/4 sin ⁡π/12 cos π/12.cos π/12

= 96√3.1/8.sin π/6.cos⁡π/6 = 6√3.sin⁡π/3=9

c) 9° + 81° = 90°

63° + 27° = 90°

=> tan81° = cot9°

tan63° = cot27°

Do đó tan9° – tan63° + tan81° – tan27° = tan9° + cot9° – (cot27° + tan27°)