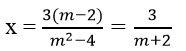Giải và biện luận các phương trình sau theo tham số m

Bài 2: Phương trình quy về phương trình bậc nhất, bậc hai

Bài 2 trang 62 Toán 10: Giải và biện luận các phương trình sau theo tham số m

a) m(x – 2) = 3x + 1

b) m²x + 6 = 4x + 3m

c) (2m + 1)x – 2m = 3x – 2

Trả lời

a) m(x – 2) = 3x + 1 (1)

⇔ mx – 3x = 2m + 1

⇔ (m – 3)x = 2m + 1 (2)

m – 3 ≠ 0 ⇔ m ≠ 3; (2) ⇔ x = (2m+1)/(m-3)

m – 3 = 0 ⇔ m =3; (2) ⇔ 0x = 7 (vn)

Tóm lại:

* Khi m ≠ 3 thì (1) có tập nghiệm T = {(2m+1)/(m-3)}

* Khi m = 3 thì (1) có T = ∅

b) m²x + 6 = 4x + 3m (1)

⇔ (m2 – 4)x = 3m – 6 (2)

* (m² – 4) ≠ 0 ⇔ m ≠ ±2 => (1) ⇔

* m² – 4 = 0 ⇔ m = ± 2 => (2) ⇔ 0x = 0: T = R

0x = -12; T = ∅

Tóm lại:

Khi m ≠ ±2 thì (1) có T = {3/(m+2)}

Khi m = 2 thì (1) có T = R

Khi m = -2 thì (1) có T = ∅

c) (2m + 1)x – 2m = 3x – 2 (1)

⇔ 2(m – 1)x = 2(m – 1) (2)

m – 1 ≠ 0 ⇔ m ≠ 1 => (2) ⇔ x = 1

m – 1 = 0 ⇔ m = 1; 0x = 0: T = R

Vậy:

Khi m ≠ 1, (1) có T = {1}

Khi m = 1, (1) có T = R.