Giải các phương trình x^2 + 3x + 2 / 2x + 3 = 2x - 5 / 4

Bài 2: Phương trình quy về phương trình bậc nhất, bậc hai

Bài 1 trang 62 Toán 10: Giải các phương trình

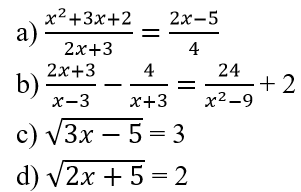
Trả lời

a) * Tập xác định: 2x + 3 ≠ 0 ⇔ x ≠ (-3)/2

* Quy đồng và bỏ mẫu chung:

4(x² + 3x + 2) = (2x – 5)(2x + 3)

⇔ 16x = 23 ⇔ x = (-23)/16 (nhận)

Vậy T = {(-23)/16}

b) * Tập xác định: x² – 9 ≠ 0 ⇔ x ± 3

* Quy đồng và bỏ mẫu chung:

(x + 3)(2x + 3) – 4(x – 3) = 24 + 2(x2 – 9) ⇔ x = -3 (loại)

Vậy T = ∅

c) * Tập xác định: √(3x-5) tồn tại ⇔ 3x – 5 ≥ 0 ⇔ x ≥ 5/3

* Bình phương hai vế: √(3x-5) = 3 ⇔ 3x – 5 = 9 ⇔ x = 14/3 (nhận)

Vậy tập nghiệm T = {14/3}

d) * Tập xác định: 2x + 5 ≥ 0 ⇔ x ≥ (-5)/2

* Bình phương hai vế: 2x + 5 = 4 ⇔ x = -1/2 (nhận)

* Tập nghiệm: T = {-1/2}