Xác định parabol y = ax^2 + bx + 2, biết rằng parabol đó

---

Bài 3: Hàm số bậc hai

Bài 3 trang 49 Toán 10: Xác định parabol y = ax² + bx + 2, biết rằng parabol đó

a) Đi qua hai điểm M(1; 5) và N(-2; 8)

b) Đi qua điểm A(3; -4) và có trục đối xứng là x = - 3/2

c) Có đỉnh là I(2; -2)

d) Đi qua điểm B(-1; 6) và có tung độ đỉnh là – 1/4

Trả lời

Phương pháp

* M(x₀; y₀) ∈ (P): y = ax² + bx + c (a ≠ 0)

⇔ y₀ = ax₀² + bx₀ + c

* Tính a, b, c từ các phương trình tìm được

a) (P): y = ax² + bx + 2 (a ≠ 0)

* M(1; 5) ∈ (P) ⇔ 5 = a + b + 2 (1)

* N(-2; 8) ∈ (P) ⇔ 8 = a(-2)2 + b(-2) + 2 ⇔ 4 = 2a – b + 1 (2)

Giải hệ (1) và (2) ta được a = 2, b = 1

Vậy (P): y = 2x² + x + 2

b) (P): y = ax² + bx + 2

* A(3; -4) ∈ (P) ⇔ -4 = 9a + 3b + 2 (1)

* Trục đối xứng x = - 3/2 ⇔ - b/2a=-3/2 ⇔ b = 3a (2)

Vậy (P): y = - 1/3x² – x + 2

c) (P): y = ax² + bx + 2 (a ≠ 0)

* Đỉnh I(2; -2). Mà đỉnh S( - b/2a;-Δ/4a)

nên - b/2a=2 (a≠0)

⇔ b = -4a (1)

* Mặt khác, I(2;-2) ∈ (P) ⇔ -2a = 4a + 2b + 2

⇔ -2 = 2a + b (2)

Giải hệ (1) và (2) ta được a = 1; b = -4

Vậy (P): y = x² – 4x + 2

Chú ý: Ở đây I(2; -2) là đỉnh của (P)

Từ giả thiết này, ta có thể sử dụng

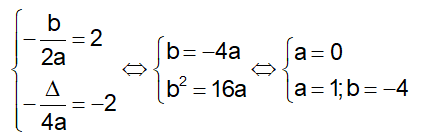
Vậy (P): y = x² – 4x + 2

d) (P): y = ax² + bx + 2 (a ≠ 0)

* B(-1; 6) ∈ (P) ⇔ 4 = a – b (1)

* Tung độ của đỉnh: - 1/4. Mà tung độ của đỉnh là - Δ/4a nên - Δ/4a = - 1/4.

⇔ Δ = a

⇔ b² – 8a = a ⇔ b² = 9a (2)

Giải hệ (1) và (2) ⇒ a = 1 và a = 16

Với a = 1 và b = -3, (P): y = x² – 3x + 2

Với a = 16 và b = 12, (P): y = 16x² – 12x + 2