Trên đường tròn lượng giác cho điểm M xác định bởi sđ cung AM

Bài 1: Cung và góc lượng giác

Bài 7 trang 140 Toán 10: Trên đường tròn lượng giác cho điểm M xác định bởi sđ cung AM = α (0 < α < π/2). Gọi M₁, M₂, M₃ lần lượt là điểm đối xứng của M qua trục Ox, trục Oy và gốc tọa độ. Tìm số đo của các cung AM₁, AM₂, AM₃.

Trả lời

Theo đề bài, sđ cung AM = α (0 < α < π/2) => sđ cung AM = α

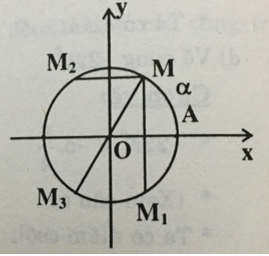
Do đó: (với k, l, m ∈ Z)

sđ cung AM₁ = - α + k.2π (vì sđ cung AM₁ = sđ cung AM)

sđ cung AM₂ = (π - α ) + l.2π (vì sđ cung AM₂ = π – α

sđ cung AM₃ = π + α + m2π (vì sđ cung AM₃ = π + α