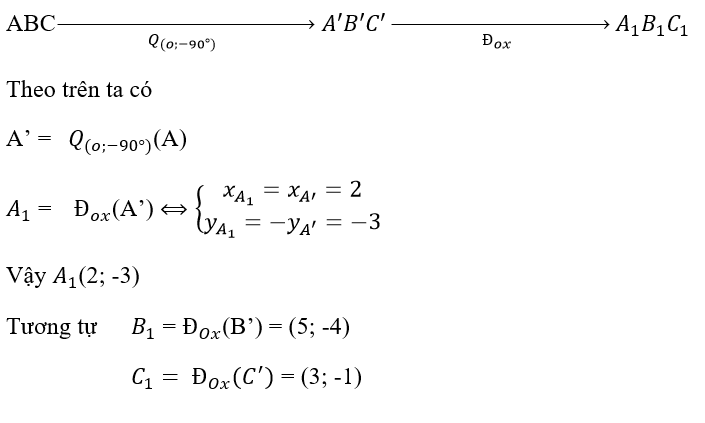Trong mặt phẳng Oxy cho các điểm A(-3; 2); B(-4; 5); C(-1; 3) Chứng minh rằng các

Bài 6: Khái niệm về phép dời hình và hai hình bằng nhau

Bài 1 trang 23 Toán 11: Trong mặt phẳng Oxy cho các điểm A(-3; 2); B(-4; 5); C(-1; 3).

a) Chứng minh rằng các điểm A’(2;3); B’(5; 4); C’(3; 1) theo thứ tự là ảnh của A, B, C qua phép quay tâm O góc -90º.

b) Gọi tam giác A₁B₁C₁ là ảnh của tam giác ABC qua phép dời hình có được bằng cách thực hiên liên tiếp phép quay tâm O góc -90º và phép đối xứng qua trục Ox. Tìm tọa độ các đỉnh của A₁B₁C₁.

Trả lời

a) Để chứng minh A’(2; 3) là ảnh của điểm A(-3; 2) trong phép quay tâm O góc -90º ta cần chứng minh:

Khi biến A → A’ xoay theo chiều âm của mặt phẳng

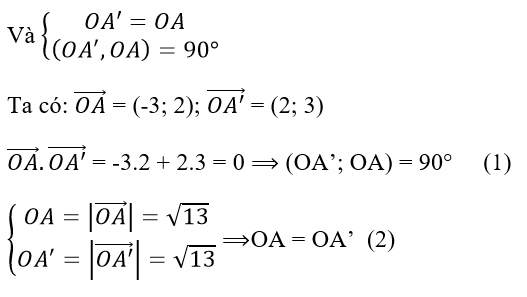
Vì A(-3; 2), x < 0, y > 0 nên điểm A thuộc góc phần tư thứ hai và A’(2; 3), x > 0, y > 0 nên điểm A’ thuộc góc phần tư thứ nhất.Do đó khi biến A → A’ ta phải quay theo chiều âm của mặt phẳng.     (3)

Từ (1)(2)(3) ⇒ A’ = Q_{(O; -90º)}(A)

Tương tự B’ = Q_{(O; -90º)}(B) và C’ = Q_{(O; -90º)}(C)

b) Theo bài ra ta có: