Trên hình 49, ta có hai đường tròn (A; 2cm) và (B; 2cm) cắt nhau tại C,D

Bài 8: Đường tròn

Bài 39 trang 92 Toán 6 Tập 2: Trên hình 49, ta có hai đường tròn (A; 2cm) và (B; 2cm) cắt nhau tại C,D, AB = 4 cm. Đường tròn tâm A,B lần lượt cắt đoạn thẳn AB tại K,I.

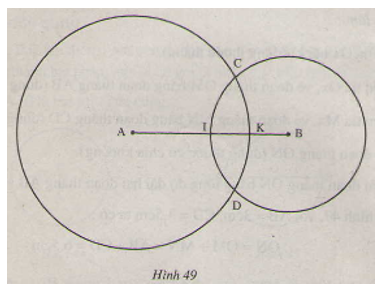
a) Tính CA, CB, DA, DB.

b) I có phải là trung điểm của đoạn thẳng AB không?

c) Tính IK.

Trả lời

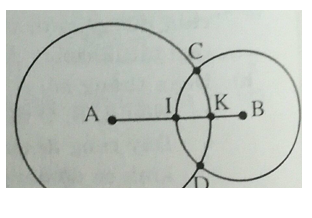
a) Tính CA, CB, DA, DB

Hai đường tròn (A; 3cm) và (B; 2cm) cắt nhau tại

C và D nên C và D vừa thuộc (A; 3cm) và vừa thuộc (B; 2cm)

Do đó CA = DA = 3cm = bán kính của (A)

CB = DB = 2cm bán kính của (B)

b) Điểm I là trung điểm của AB

Ta chứng minh

   +) I nằm giữa hai điểm A và B

   +) IA = IB

⇒ I là trung điểm của AB

Đường tròn tâm B cắt AB tại I nên BI = 2cm = bán kính

Ta có BA= 4 cm (gt) ⇒ BI < BA ⇒ I nằm giữa A và B (1)

⇒ IA + IB = AB hay IA + 2cm = 4cm ⇒ IA = 4cm - 2cm = 2cm

Do đó IA = IB = 2cm

Từ (1) và (2) ta có I là trung điểm của AB

c) Tính IK

Ta có AK là bán kính của đường tròn (A; 3cm) nên AK = 3cm

Ta đã có IA = 2cm ⇒ AI < AK nên điểm I nằm giữa hai điểm A và B

⇒ IA +IK = AK hay 2cm + IK = 3cm

⇒ IK = 3cm – 2cm = 1cm

Vậy IK =1cm