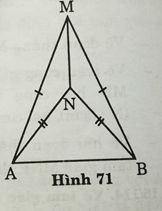
Xét bài toán: tam giác AMB và tam giác ANB có MA = MB, NA = NB hình 71

Giải bài tập Toán lớp 7 Luyện tập (trang 114-115)

Bài 18 trang 114 Toán lớp 7 Tập 1: Xét bài toán: "ΔAMB và ΔANB có MA = MB,NA = NB (h.71). Chứng minh rằng AMN = BMN."

1) Hãy ghi giả thiết và kết luận của bài toán.

2) Hãy sắp xếp bốn câu sau đây một cách hợp lý để giải bài toán trên:

a) Do đó ΔAMN = ΔBMN (c.c.c)

b)

MN cạnh chung

MA = MB ( Giả thiết)

NA = NB ( Giả thiết)

c) Suy ra AMN = BMN (2 góc tương ứng)

d) ΔAMB và ΔANB có:

Trả lời

1. Ghi giả thiết và kết luận:

2. Sắp xếp hợp lí để giải bài toán

d) ΔAMB và ΔANB có:

b)

MN cạnh chung

MA=MB ( Giả thiết)

NA=NB ( Giả thiết)

a) Do đó ΔAMN = ΔBMN (c.c.c)

c) Suy ra AMN = BMN (2 góc tương ứng)