Xét bài toán: Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của MA
Toán lớp 7 Bài 4: Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh (c.g.c)
Bài 26 trang 118 Toán lớp 7 Tập 1: Xét bài toán:
" Cho tam giác ABC, M là trung điểm của BC, Trên tia đối của MA lấy điểm E sao cho ME = MA. Chứng minh rẳng AB//CE".
Dưới đây là hình vẽ và giả thiết, kết luận của bài toán(h.85)
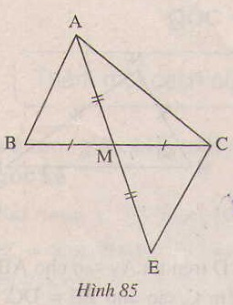
| GT | ΔABC ; MB=MC ; MA=ME |
| KL | AB//CE |
Hãy sắp xếp lại năm câu sau đây một cách hợp lí để giải bài toán trên:
1) MB = MC (gt)
AMB = EMC (Hai góc đối đỉnh)
MA = ME(Giả thiết)
2) Do đó ΔAMB = ΔEMC(c.g.c)
3) MAB = MEC => AB//CE (hai góc bằng nhau ở vị trí sole trong)
4) ΔAMB = ΔEMC => AB // CE (Hai góc tương ứng)
5) ΔAMB và ΔEMC có:
Lưu ý để cho gọn, các quan hệ nằm giữa, thẳng hàng (như M nằm giữa B và C, E thuộc tia đối của tia MA) đã được thể hiện ở hình vẽ nên có thể không ghi ở phần giả thiết.
Trả lời
5) ΔAMB và ΔEMC có:
1) MB = MC (gt)
AMB = EMC (Hai góc đối đỉnh)
MA = ME(Giả thiết)
2) Do đó ΔAMB = ΔEMC(c.g.c)
4) ΔAMB = ΔEMC => AB // CE (Hai góc tương ứng)
3) MAB = MEC => AB//CE (hai góc bằng nhau ở vị trí sole trong)

