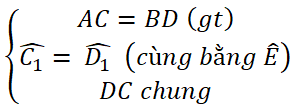Chứng minh định lý: Hình thang có hai đường chéo bằng nhau là hình thang cân

Luyện tập (trang 75)

Bài 18 trang 75 Toán 8 Tập 1: Chứng minh định lý: “Hình thang có hai đường chéo bằng nhau là hình thang cân” qua bài toán sau: Cho hình thang ABCD (AB // CD) có AC = BD. Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại E. Chứng minh rằng:

a) Tam giác DBE là tam giác cân

b) ΔACD = ΔBDC

c) Hình thang ABCD là hình thang cân

Trả lời

a) Xét hai tam giác ABC và ECB có:

∠ABC = ∠ECB (sole trong)

BC chung

∠BCA = ∠EBC (sole trong)

Do đó ΔECB = ΔABC (g.c.g)

⇒AC = BE      (1)

Còn có AC = BD (gt)     (2)

Từ (1) và (2) ⇒ BD = BE. Vậy tam giác BDE cân tại B

b) Xét hai tam giác ACD và BDC có

Do đó ΔACD = ΔBDC

d) ΔACD = ΔBDC (cmt) ⇒ ∠ADC = ∠BCD ⇒ ABCD là hình thang cân