Phân tích các đa thức sau thành nhân tử x^3 + 1/27
Bài 7: Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
Bài 44 trang 20 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử.
a) x3 + 1/27 b) (a+b)3 – (a-b)3
c) (a+b)3+(a-b)3 d) 8x3 + 12x2y + 6xy2 + y3
e) –x3 + 9x2 – 27x + 27
Trả lời
a) Áp dụng A3 + B3 = (A + B) (A2 – AB + B2 )
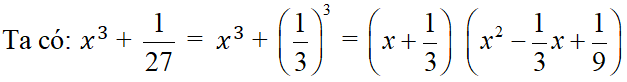
b) Áp dụng A3 – B3= (A – B) (A2+ AB + B2)
Ta có: (a+b)3 – (a-b)3
= [a + b – (a – b)] [(a+b)2 + (a+b)(a-b)+(a-b)2]
= 2b (a2 + 2ab + b2 + a2–b2+ a2– 2ab +b2 = 2b.(3a2+b2)
c) Áp dụng A3 + B3 = (A + B) (A2– AB +B2) với A = (a + b), B = (a – b)
Ta có: (a+b)3 + (a-b)3
= [a + b + a – b] [(a+b)2 – (a+b)(a-b) +(a-b)2]
= 2b (a2+ 2ab + b2 - a2 + b2 + a2– 2ab + b2 )= 2a(a2+3b2)
d) Áp dụng (A+B)3 = A3 + 3A2B + 3AB2 + B3
Ta có: 8x3 + 12x2y + 6xy2 + y3 = (2x)3 +3(2x)2 y+3.2x.y2 +y3
e) Áp dụng (A+B)3 = A3 - 3A2B + 3AB2 - B3
Ta có: -x3 + 9x2 – 27x + 27 = – (x3– 9x2 + 27x – 27)
= – (x3– 3.x2.3 + 3. x. 32– 27)
= – (x- 3)3

