Ở hình 51, tam giác ABC vuông ở A và có đường cao AH

Luyện tập (trang 84-85)

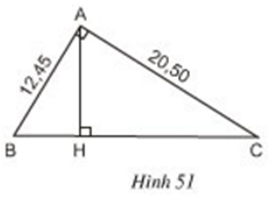
Bài 49 trang 84 Toán 8 Tập 2: Ở hình 51, tam giác ABC vuông ở A và có đường cao AH.

a) Trong hình vẽ có bao nhiêu cặp tam giác đồng dạng với nhau? (Hãy chỉ rõ từng cặp tam giác đồng dạng và viết theo các đỉnh tương ứng).

b) Cho biết AB = 12,45cm, AC = 20,50cm. Tính độ dài các đoạn thẳng BC, AH, BH và CH.

Trả lời

a) Các cặp tam giác đồng dạng có trong hình 51 là:

ΔAHB ∼ ΔCAB ( hai tam giác vuông có góc B chung)

ΔCHA ∼ ΔCAB ( hai tam giác vuông có góc C chung)

ΔAHB ∼ ΔCHA ( vì cùng đồng dạng với tam giác CAB)

b) Áp dụng định lí Pi-ta-go vào tam giác ABC vuông tại A ta có:

BC² = AB² + AC² = (12,45)² + (20,5)² = 575,25

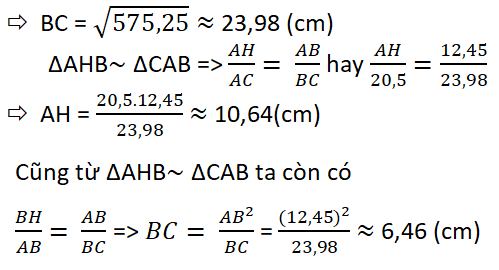
Do đó CH = BC - BH = 23,98 – 6,46 = 17,52 (cm)

Vậy BC = 23,98cm ; AH = 10,64cm; BH = 6,46cm; CH = 17,52 cm.