Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB

Luyện tập (trang 92-93)

Bài 49 trang 93 Toán 8 Tập 1: Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự M, N. Chứng minh rằng:

a) AI // CK

b) DM = MN = NB

Trả lời

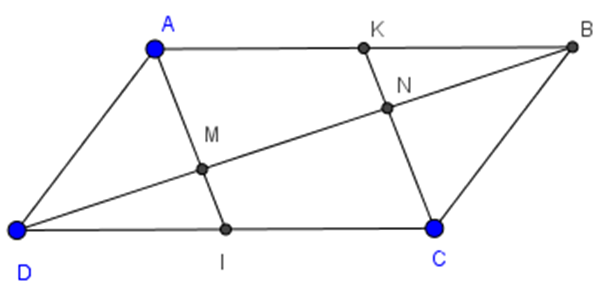
a) AI // CK

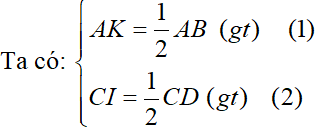
Mà AB // CD và AB = CD (cạnh đối hình bình hành ABCD)

Từ (1) và (2) suy ra AK = CI và AK // CI

⇒AKCI là hình bình hành (dấu hiệu 5) ⇒ AI // CK (đpcm)

b) DM = MN = NB

Trong tam giác BAM có KA = KB (gt) và KN // AM (cmt)

Suy ra NB = MN     (3)

Trong tam giác DCN có ID = IC (gt) và IM = CN (cmt)

Suy ra DM = MN     (4)

Từ (3) và (4) suy ra DM = MN = NB (đpcm)