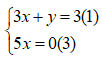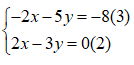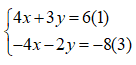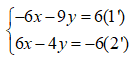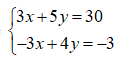Bài 20 trang 19 Toán 9 Tập 2

Bài 4: Giải hệ phương trình bằng phương pháp cộng đại số

Bài 20 trang 19 Toán 9 Tập 2: Giải các hệ phương trình sau bằng phương pháp cộng đại số

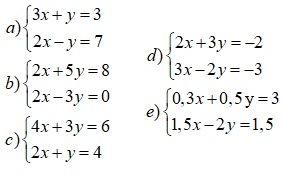
Bài giải:

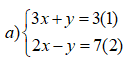
Bước 1: Cộng vế (1) và (2): 5x = 10     (3)

Bước 2: Giải hệ

(3) ⇔ x= 2

Thay x = 2 vào (1) ta có 3.2 + y = 3 ⇔ y = -3

Vậy nghiệm của hệ (2; -3)

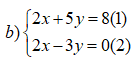
Bước 1: Nhân -1 vào hai vế của (1) ta có:

(1) ⇔ -1. (2x +5y) = -1.8 ⇔ -2x -5y = -3     (1’)

Giải hệ

Bước 2: Cộng vế của (3) và (2) ta được: -8y = -8 ⇔ y = 1

Thay y = 1 vào (2) : 2x -3.1 = 0 ⇔ x =

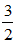
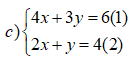
Vậy nghiệm của hệ (;1)

Bước 1: Nhân (-2) vào hai vế của (2) ta được:

-2(2x+y) = -2 ⇔ -4x -2y = -8     (3)

Bước 2: Giải hệ

Cộng vế (1) và (2) ta được y = -2

Thay y = -2 vào (1) ta có x = 3

Vậy nghiệm của hệ (3; -2)

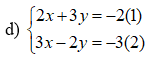
Bước 1: Nhân (-3) vào hai vế của (1) và (2) ta có:

Cộng vế (1’) và (2’) ta được -13y= 0 ⇔ y = 0

Thay y = 0 vào (1) ta được x = -1

Vậy hệ có nghiệm (-1;0)

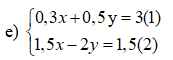
Bước 1: Nhân 10 vào hai vế của (1) ta có: 3x + 5y = 30     (1’)

Nhân -2 vào 2 vế của (2) ta có: -3x + 4y = -3     (2’)

Bước 2: Giải hệ

Cộng vế theo vế (1’) và (2’) ta được 9y = 27 ⇔ y = 3

Thay y = 3 vào (1’) ta được x = 5

Vậy nghiệm của hệ (5; 3)

Chú ý:

1) Tìm cách biến hệ số của x (hoặc của y) ở hai phương trình của hệ thành hai số bằng nhau (hoặc đối nhau)

2) Nếu hai số bằng nhau, ta trừ vế; nếu hai số đối nhau, ta cộng vế.