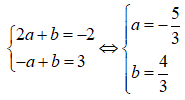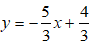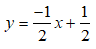Bài 26 trang 19 Toán 9 Tập 2

Luyện tập (trang 19-20)

Bài 26 trang 19 Toán 9 Tập 2: Xác định a và b để đồ thị của hàm số y = ax + b đi qua hai điểm A và B trong môi trường hợp sau:

a) A(2; -2) và B(-1; 3)

b) A(-4; -2) và B(2; 1)

c) A(3;-1) và B(-3; 2)

d) A(√3; 2) và B(0; 2)

Bài giải:

Phương pháp: Áp dụng: Đường thẳng (d): y = ax + b (a ≠ 0) đi qua A(x_A; y_A) ⇔ y_A = ax_A + b

a) A(2; -2) và B(-1; 3)

Đường thẳng đi qua A(x_A; y_A) ⇔ y_A = ax_A + b

Mà x_A = 2 và y_A = -2 (gt) nên ta có: -2 = a(2) + b ⇔ 2a + b = -2     (1)

Tương tự, đường thẳng đi qua B(x_B; y_B) ⇔ y_B = ax_B + b

Mà x_B = -1 và y_B = 3 (gt) nên ta có: 3 = a(-1) + b ⇔ -a + b = 3     (2)

Giải hệ tạo bởi (1) và 2):

Vậy đường thẳng qua A và B có phương trình:

b) Đường thẳng (d) qua A(-4; -2) và B(2; 1) có phương trình: y = ax +b (a ≠ 0)     (*)

* Vì (d) qua A(-4; -2) nên (*) ⇒ -2 = -4a + b     (1)

* Vì (d) qua B(2; 1) nên (*) ⇒ 1 = 2a + b     (2)

Hệ tạo bởi (1) và (2) có nghiệm a = 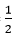và b = 0

Vậy (d): y = 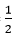x

c) Đường thẳng (d) qua A(3; -1) và B(-3; 2) có phương trình dạng: y = ax + b (a ≠ 0)     (*)

* Vì A(3; -1) ∈ (d) nên (*) ⇔ -1 = 3a + b     (1)

* Vì B(-3; 2) ∈ (d) nên (*) ⇒ 2 = -3a + b     (2)

Giải hệ tạo bởi (1) và (2) ta được a = -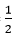; b =

Vậy phương trình của (d):

d) (d) qua A và B nên y_A = ax_A + b ⇔ 2 = a√3 + b     (1)

và y_B = ax_B + b ⇔ 2 = b     (2)

Thay b = 2 ở (2) vào (1) ta được a = 0

Vậy (d): y = 2