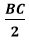Bài 39 trang 123 Toán 9 Tập 1

Luyện tập (trang 123)

Bài 39 trang 123 Toán 9 Tập 1: Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC, B ∈ (O) và C ∈ (O’). Tiếp tuyến chung tại A cắt tiếp tuyến chung ngoài BC tại I.

a) Chứng minh rằng ∠BAC = 90°

b) Tính số đo góc OIO’

c) Tính độ dài BC biết OA = 9cm, O’A = 4cm

Bài giải:

a) Ta có: IA = IB (tiếp tuyến của (O) phát xuất từ I)     (1)

Tương tự, IA = IC     (2)

(1) và (2) ⇒ I là trung đỉểm của BC. Suy ra AI là trung tuyến của ΔABC.

Cũng từ (1) và (2), ta có: AI =

Tóm lại, tam giác ABC có trung tuyến AI bằng nửa cạnh tương ứng BC nên ΔABC vuông tại A.

b) Tính số đo góc OIO'

Ta có: IA và IB là hai tiếp tuyến của (O) cùng phát xuất từ I.

⇒ IO là tia phân giác của ∠BIA

Tương tự, IO' là tia phân giác của ∠CIA

Mà ∠BIA và ∠CIA là hai góc kề và bù nên IO ⊥ IO’

Vậy, ∠OIO' = 90°

c) Độ dài BC.

ΔOIO' vuông tại I có AI là đường cao (AI là tiếp tuyến của (O) tại A).

⇒ IA² = AO.AO ⇒ IA = 6cm

Suy ra, vì BC = 2IB nên BC = 2IA ⇒ BC = 6cm.