Lập bảng biến thiên và vẽ đồ thị của hàm số bậc hai. y = 2x^2 + 4x - 6. y = -3x^2 - 6x + 4

Bài 3: Hàm số bậc hai

Bài 2.19 trang 41 Sách bài tập Đại số 10: Lập bảng biến thiên và vẽ đồ thị của hàm số bậc hai

    a) y = 2x² + 4x - 6;

    b) y = -3x² - 6x + 4;

    c) y = √3x² + 2√3x + 2;

    d) y = -2(x² + 1)

Lời giải:

    a) Hàm số bậc hai đã cho có a = 2; b = 4; c = -6;

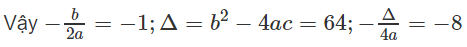
    Vì a > 0, ta có bảng biến thiên

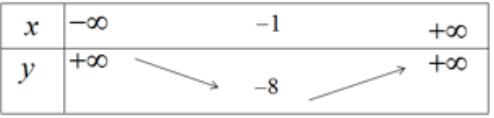
    Hàm số nghịch biến trên khoảng (-∞; -1) đồng biến trên khoảng (-1; +∞)

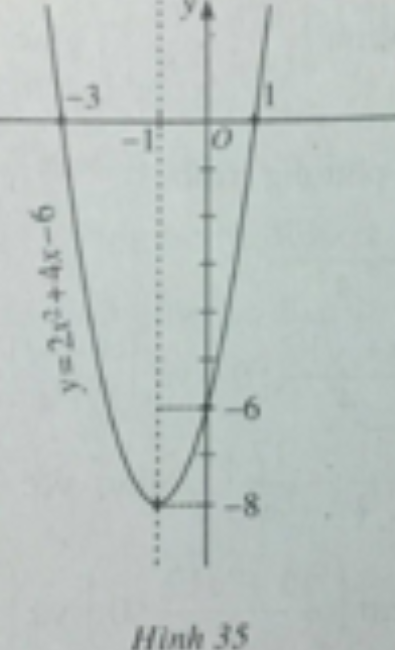
    Để vẽ đồ thị ta có trục đối xứng là đường thẳng x = -1; đỉnh I(-1;-8); giao với tục tung tại điểm (0;-6); giao với trục hoành tại các điểm (-3;0) và (1;0).

    Đồ thị của hàm số y = 2x² + 4x - 6 được vẽ trên hình 35.

    b) Bảng biến thiên

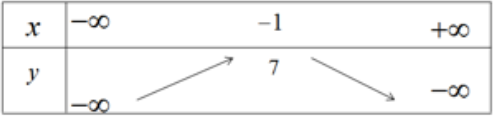
    Hàm số đồng biến trên khoảng (-∞; -1) nghịch biến trên khoảng (-1; +∞)

    Đỉnh parabol I(-1;7). Đồ thị của hàm số y = -3x² - 6x + 4 được vẽ trên hình 36.

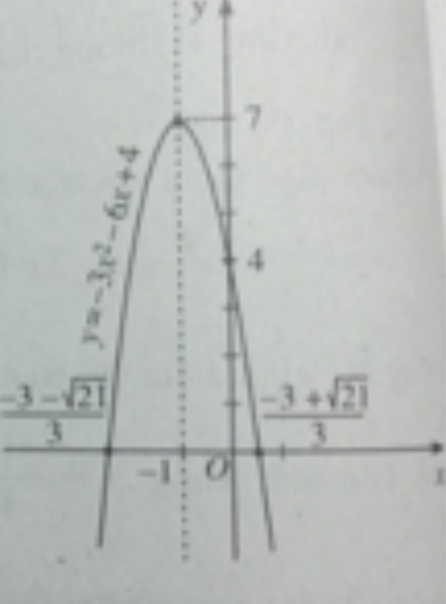
    c) Bảng biến thiên

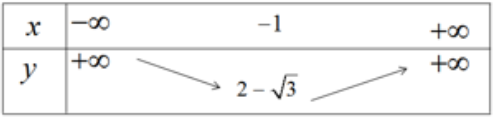
    Hàm số nghịch biến trên khoảng (-∞; -1) đồng biến trên khoảng (-1; +∞)

    Đỉnh parabol (-1; 2 - √3)

    Đồ thị hàm số được vẽ trên hình 37.

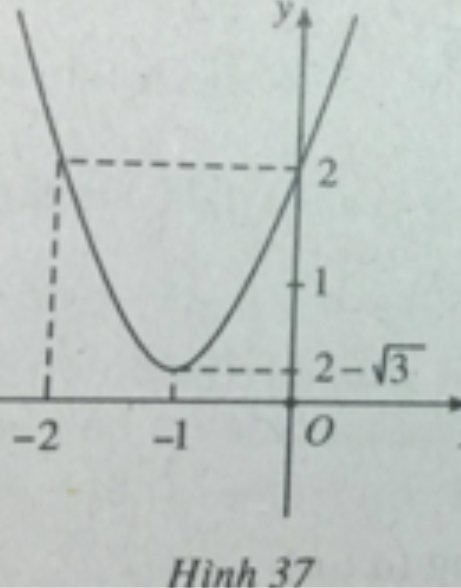
    d) Bảng biến thiên

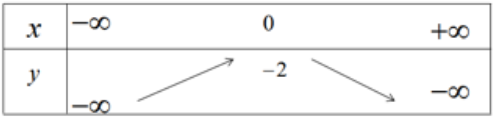
    Hàm số đồng biến trên khoảng (-∞; 0) nghịch biến trên khoảng (0; +∞), hàm số là chẵn.

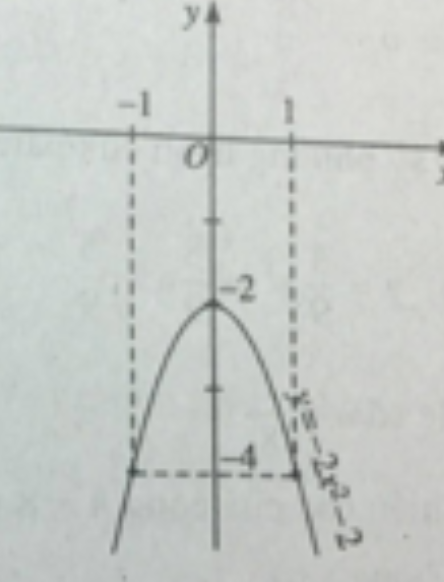
    Đỉnh parabol I(0;-2); đồ thị đi qua điểm (1;-4) và điểm (-1;-4).

    Đồ thị hàm số y = -2(x² + 1) được vẽ trên hình 38.