Cho tam giác ABC nội tiếp trong đường tròn tâm O, H là trực tâm của tam giác

Bài 3: Tích của vectơ với một số

Bài 1.35 trang 32 Sách bài tập Hình học 10: Cho tam giác ABC nội tiếp trong đường tròn tâm O, H là trực tâm của tam giác, D là điểm đối xứng của A qua O.

    a) Chứng minh tứ giác HCDB là hình bình hành.

    b) Chứng minh:

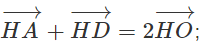
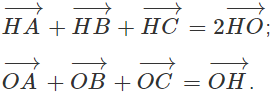
    c) Gọi G là trọng tâm tam giác ABC.

    Chứng minh

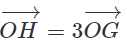
    Từ đó có kết luận gì về ba điểm O, H, G?

Lời giải:

    (Xem h.1.55)

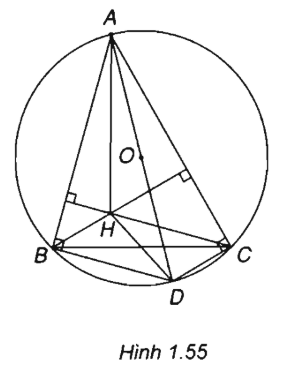
    a) Vì AD là đường kính của đường tròn tâm O nên BD ⊥ AB, DC ⊥ AC

    Ta có CH ⊥ AB, BH ⊥ AC nên suy ra CH // BD và BH // DC

    Vậy tứ giác HCDB là hình bình hành.

    b) Vì O là trung điểm của AD nên

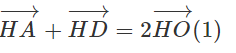
    Vì tứ giác HCDB là hình bình hành nên ta có

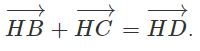
    Vậy từ (1) suy ra:

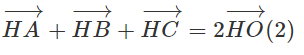
    Theo quy tắc ba điểm, từ (2) suy ra

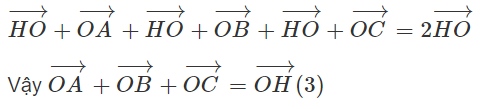
    c) G là trọng tâm của tam giác ABC.

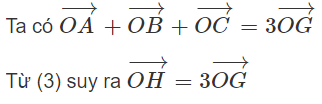
    Vậy ba điểm O, H, G thẳng hàng.

    Trong một tam giác trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O thẳng hàng.