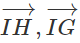Trong mặt phẳng Oxy, cho tam giác ABC với A(2; 4); B(3; 1); C(-1; 1). Tìm tọa độ trọng tâm G, trực tâm H

Ôn tập chương 2

Bài 2.57 trang 105 Sách bài tập Hình học 10: Trong mặt phẳng Oxy, cho tam giác ABC với A(2; 4); B(3; 1); C(-1; 1).

    a) Tìm tọa độ trọng tâm G, trực tâm H, tâm I của đường tròn ngoại tiếp tam giác ABC;

    b) Chứng minh H, G, I thẳng hàng.

Lời giải:

    A(2;4), B(3;1), C( - 1;1)

    a) Tọa độ trọng tâm G của tam giác ABC là:

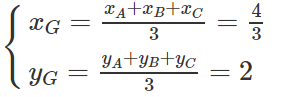
    Vậy G(4/3; 2)

    Goi H(x; y), ta có:

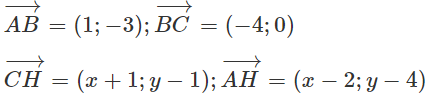
    H là trực tâm tam giác ABC

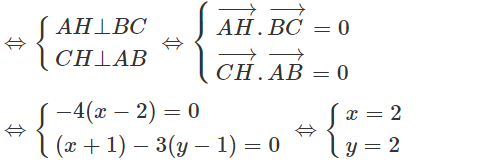
    Gọi I(x; y), I là tâm đường tròn ngoại tiếp tam giác ABC ⇔ IA = IB = IC

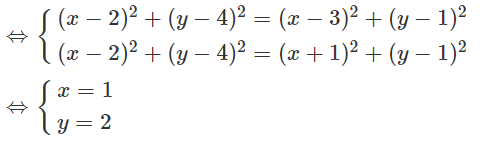
    Vậy: I(1; 2)

    b) Ta có:

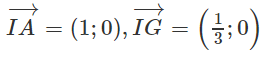
    ⇒ cùng phương nên H, G, I thẳng hàng.