Cho tam giác ABC có AB = c, AC = b (với b ≠ c) phân giác trong AD = k (D nằm trên cạnh BC)

Ôn tập chương 2

Bài 2.59 trang 105 Sách bài tập Hình học 10: Cho tam giác ABC có AB = c, AC = b (với b ≠ c) phân giác trong AD = k (D nằm trên cạnh BC), BD = d, CD = e. Chứng minh hệ thức: k² = bc - de

Lời giải:

    Ta có AD là phân giác trong góc A của tam giác ABC nên góc BAD = góc DAC

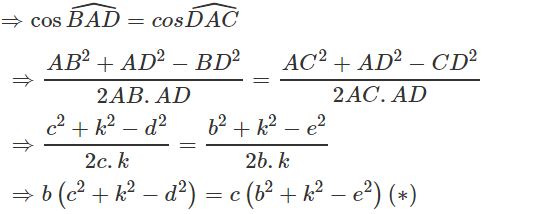
    Vì AD là phân giác trong góc A của tam ABC nên

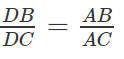
    ⇒ bd = ce, từ (∗) ta suy ra (b - c)(-k² + bc - be) = 0

    ⇒ k² = bc - de (vì b ≠ c) (điều phải chứng minh)