Cho tam giác ABC, biết phương trình đường thẳng AB: x - 3y + 11 = 0, đường cao AH: 3x + 7y - 15 = 0
Bài 1: Phương trình đường thẳng
Bài 3.6 trang 148 Sách bài tập Hình học 10: Cho tam giác ABC, biết phương trình đường thẳng AB: x - 3y + 11 = 0, đường cao AH: 3x + 7y - 15 = 0, đường cao BH: 3x - 5y + 13 = 0. Tìm phương trình hai đường thẳng chứa hai cạnh còn lại của tam giác.
Lời giải:
Theo đề bài tọa độ điểm A luôn thỏa mãn hệ phương trình:
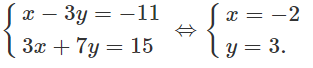
Vì AC ⊥ BH nên C có dạng: 5x + 3y + c = 0, ta có:
A ∈ AC ⇔ -10 + 9 + c = 0 ⇔ c = 1
Vậy phương trình đường thẳng chứa cạnh AC: 5x + 3y + 1 = 0.
Tọa độ của điểm B luôn thỏa mãn hệ phương trình:
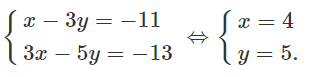
Vì BC ⊥ AH nên BC có dạng: 7x - 3y + c = 0, ta có:
B ∈ BC ⇔ 28 - 15 + c = 0 ⇔ c = -13
Vậy phương trình đường thẳng chứa cạnh BC: 7x - 3y - 13 = 0.

