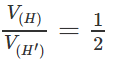Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, AA’ = c. Gọi E và F lần lượt là những điểm

Bài 3: Khái niệm về thể tích của khối đa diện

Bài 1.16 trang 19 Sách bài tập Hình học 12: Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, AA’ = c. Gọi E và F lần lượt là những điểm thuộc cạnh BB’ và DD’ sao cho BE = EB′/2, DF = FD′/2. Mặt phẳng (AEF) chia khối hộp chữ nhật ABCD.A’B’C’D’ thành hai khối đa diện (H) và (H’). Gọi (H’) là khối đa diện chứa đỉnh A’. Hãy tính thể tích của (H) và tỉ số thể tích của (H) và (H’).

Lời giải:

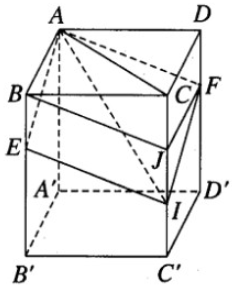
Giả sử (AEF) cắt CC’ tại I. Khi đó ta có AE// FI, AF // EI nên tứ giác AEIF là hình bình hành. Trên cạnh CC’ lấy điểm J sao cho CJ = DF. Vì CJ song song và bằng DF nên JF song song và bằng CD. Do đó tứ giác CDFJ là hình chữ nhật. Từ đó suy ra FJ song song và bằng AB. Do đó AF song song và bằng BJ. Vì AF cũng song song và bằng EI nên BJ song song và bằng EI.

Từ đó suy ra IJ = EB = DF = JC = c/3

Ta có

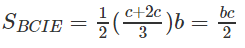
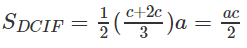
Nên V_(H) = V_A.BCIE + V_A.DCIF

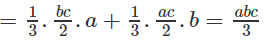
Vì thể tích khối hộp chữ nhật ABCD.A’B’C’D’ bằng abc nên

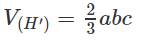
Từ đó suy ra