Xác định giá trị của tham số m để hàm số sau có cực trị: y = x^3 + 2mx^2 + mx − 1

Bài 2: Cực trị của hàm số

Giải bài 21 trang 16 SBT Giải tích 12 Bài 2: Cực trị của hàm số giúp học sinh biết cách làm bài tập trong SBT Toán 12.

Bài 1.21 trang 16 Sách bài tập Giải tích 12: Xác định giá trị của tham số m để hàm số sau có cực trị:

y = x³ + 2mx² + mx − 1

Lời giải:

TXĐ: D = R

y’ = 3x² + 4mx + m

Hàm số có cực trị khi và chỉ khi y’ đổi dấu trên R.

⇔ 3x² + 4mx + m có hai nghiệm phân biệt.

⇔ Δ’ = 4m² -3m > 0 ⇔ m(4m – 3) > 0

⇔

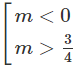
Vậy hàm số đã cho có cực đại, cực tiểu khi m < 0 hoặc m > 3/4.