Bài tập trắc nghiệm trang 16, 17 Sách bài tập Giải tích 12

Giải bài tập trắc nghiệm trang 16, 17 SBT Giải tích 12 Bài 2: Cực trị của hàm số giúp học sinh biết cách làm bài tập trong SBT Toán 12.

---

Bài 2: Cực trị của hàm số

Bài tập trắc nghiệm trang 16, 17 Sách bài tập Giải tích 12:

Bài 1.26: Hàm số y = (x + 1)³(5 - x) có mấy điểm cực trị?

A. 0              B. 1

C. 2              D. 3

Bài 1.27: Hàm số y = x⁴ - 5x² + 4 có mấy điểm cực đại?

A. 0              B. 2

C. 3              D. 1

Bài 1.28: Xác định giá trị của tham số m để hàm số y = x³ - 3x² + mx - 5 có cực trị:

A. m = 3              B. m ∈ [3; +∞]

C. m < 3              D. m > 3

Bài 1.29: Xác định giá trị của tham số m để hàm số có cực trị:

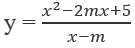
A. m > √5              B. m < -√5

C. m = √5              D. -√5 < m < √5

Bài 1.30: Cho hàm số y = -x⁴ + 4x² - 3. Khẳng định nào sau đây là đúng?

A. Hàm số có một cực đại và một cực tiểu

B. Hàm số có hai cực đại và một cực tiểu

C. Hàm số chỉ có một cực tiểu

D. Hàm số chỉ có một cực đại

Bài 1.31: Xác định giá trị của tham số m để hàm số sau không có cực trị

y = mx³/3 + mx² + 2(m - 1)x - 2.

A. m ≤ 0 hoặc m ≥ 2              B. m ≥ 0

C. m ≤ 0 ≤ 2              D. m ∈ [0; +∞]

Bài 1.32: Xác định giá trị của tham số m để hàm số sau có cực trị

y = x³ - 3(m - 1)x² - 3(m + 3)x - 5

A. m ≥ 0              B. m ∈ R

C. m < 0              D. m ∈ [-5;5]

Bài 1.33: Cho hàm số:

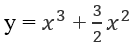
Khoảng cách d giữa hai điểm cực trị của đồ thị hàm số là:

A. d = 2√5              B. d = √5/4

C. d = √5              D. √5/2

Lời giải:

Đáp án và hướng dẫn giải

Bài	1.26	1.27	1.28	1.29	1.30	1.31	1.32	1.33
Đáp án	B	D	C	D	B	A	B	D

Bài 1.26: Đáp án: B.

Hàm số y = (x + 1)³(5 - x) xác định trên R.

y' = -(x + 1)³ + 3(x + 1)²(5 - x) = 2(x + 1)²(7 - 2x)

y' = 0 ⇔

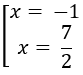
Bảng biến thiên

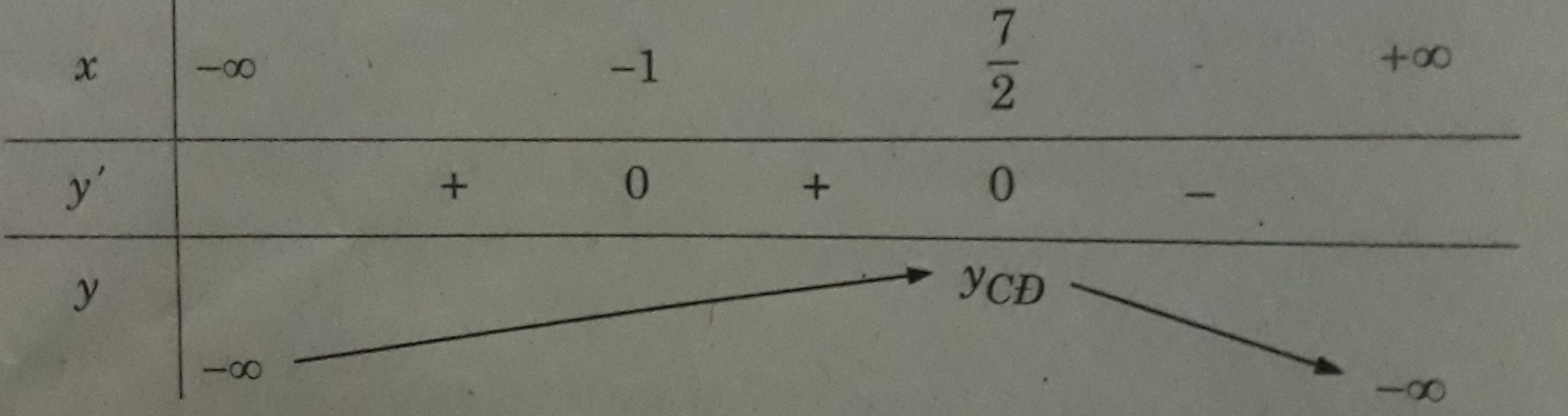
Suy ra hàm số chỉ có một cực trị (là cực đại)

Cách khác: Nhận xét rằng y' chỉ đổi dấu khi x đi qua 7/2 nên hàm số chỉ có một cực trị

Bài 1.27: Đáp án: D.

Hàm số y = x⁴ - 5x² + 4 xác định trên R.

y' = 4x³ - 10x = 2x(2x⁵ - 5);

y' = 0 khi

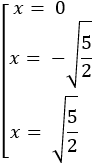
y'' = 12x² - 10

Vì y''(0) = -10 < 0,

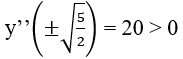
nên hàm số chỉ có một cực đại (tại x = 0)

Cách khác: Vì a > 0 và y' = 0 có ba nghiệm phân biệt nên hàm số y = ax⁴ + bx² + c có một cực đại

Bài 1.28: Đáp án: C.

Tập xác định: D = R. y' = 3x² - 6x + m.

Hàm số có cực trị khi và chỉ khi y' đổi dấu trên R

⇔ 3x² - 6x + m = 0 có hai nghiệm phân biệt

⇔ Δ' = 9 - 3m > 0 ⇔ 3m < 9 ⇔ m < 3

Bài 1.29: Đáp án: D.

Tập xác định: D = R \ {m}

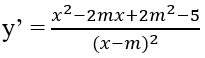
Hàm số có cực trị khi và chỉ khi y' đổi dấu trên D

⇔ x² - 2mx + 2m² - 5 = 0 có hai nghiệm phân biệt

⇔ Δ' = -m² + 5 > 0 ⇔ -√5 < m < √5

Bài 1.30: Đáp án: B.

Vì a < 0 và y' = 0 có ba nghiệm phân biệt nên hàm số y = ax⁴ + bx² + c có hai cực đại, một cực tiểu.

Ở đây y' = -4x³ + 8x; y' = 0 ⇔ -4x(x² - 2) = 0

⇔

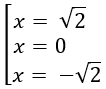
Bài 1.31: Đáp án: A.

- Nếu m = 0 thì y = -2x - 2, hàm số không có cực trị.

- Nếu m ≠ 0: Hàm số không có cực trị khi và chỉ khi phương trình y' = mx² + 2mx + 2(m - 1) = 0 không có hai nghiệm phân biệt. Muốn vậy, phải có

Δ' = m² - 2m(m - 1) = -m² + 2m ≤ 0

⇔

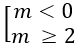
Bài 1.32: Đáp án: B.

Hàm số đã cho có cực trị khi và chỉ khi

y' = 3x² - 6(m - 1)x - 3(m + 3) = 0 có 2 nghiệm phân biệt

⇔ Δ' = (m - 1)² + (m + 3) = m² - m + 4 > 0

Ta thấy tam thức Δ' = m² - m + 4 luôn dương với mọi m vì

δ = 1 - 16 = -15 < 0, a = 1 > 0

Vậy hàm số đã cho luôn có cực trị mới mọi m ∈ R

Bài 1.33: Đáp án: D.

y' = 3x² + 3x = 3x(x + 1) = 0

⇔

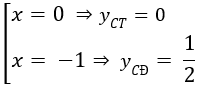
Vậy khoảng cách giữa hai điểm cực trị là: