Xác định giá trị của tham số m để hàm số sau không có cực trị

Bài 2: Cực trị của hàm số

Giải bài 25 trang 16 SBT Giải tích 12 Bài 2: Cực trị của hàm số giúp học sinh biết cách làm bài tập trong SBT Toán 12.

Bài 1.25 trang 16 Sách bài tập Giải tích 12: Xác định giá trị của tham số m để hàm số sau không có cực trị

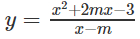
Lời giải:

Hàm số không có cực trị khi đạo hàm của nó không đổi dấu trên tập xác định R\{m}.

Ta có:

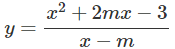
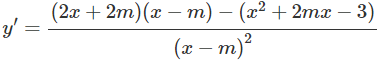
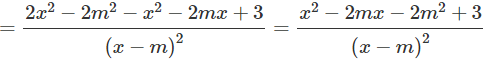
Xét g(x) = x² – 2mx – 2m² + 3

Δ’_g = m² + 2m² – 3 = 3(m² – 1) ;

Δ’_g ≤ 0 khi – 1 ≤ m ≤ 1.

Khi – 1 ≤ m ≤ 1 thì phương trình g(x) = 0 vô nghiệm hay y’ = 0 vô nghiệm và y’ > 0 trên

tập xác định. Khi đó, hàm số không có cực trị.

Khi m = 1 hoặc m = -1, hàm số đã cho trở thành y = x + 3 (với x ≠ 1) hoặc y = x – 3 (với x ≠ - 1) Các hàm số này không có cực trị.

Vậy hàm số đã cho không có cực trị khi – 1 ≤ m ≤ 1.