Tìm số phức z, biết |z| + z = 3 + 4i. Bài 4.38 trang 208 Sách bài tập Giải tích 12

Bài tập ôn tập chương 4

Bài 4.38 trang 208 Sách bài tập Giải tích 12: Tìm số phức z, biết:

a) z− = z³;

b) |z| + z = 3 + 4i.

Lời giải:

a) Ta có zz− = |z|² nên từ z− = z³ ⇒ |z|² = z⁴

Đặt z = a+ bi , suy ra:

a⁴ + b⁴ − 6a²b² + 4ab(a² − b²)i = a² + b² (∗)

Do đó, ta có: 4ab(a² − b²) = 0 (∗∗)

Từ (∗∗) suy ra các trường hợp sau:

     +) a = b = 0 ⇒ z = 0

     +) a = 0, b ≠ 0: Thay vào (∗), ta có b⁴ = b² ⇒ b = 1 hoặc b = -1 ⇒ z = i hoặc z = -1

     +) b = 0, a ≠ 0: Tương tự, ta có a = 1 hoặc a = -1 ⇒ z = 1 hoặc z = -1

     +) a ≠ 0, b ≠ 0 ⇒ a² − b² = 0⇒ a² = b², thay vào (∗) , ta có:

2a²(2a² + 1) = 0, không có a nào thỏa mãn (vì a ≠ 0 )

b) Đặt z = a + bi. Từ |z| + z = 3 + 4i suy ra

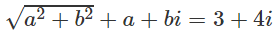
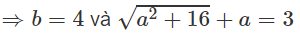
⇒ a² + 16 = (3 − a)² = 9 − 6a + a²

⇒ 6a = −7 ⇒ a = −7/6

Vậy z = −7/6 + 4i