Tìm các tiệm cận đứng và ngang của đồ thị mỗi hàm số sau: y = (x^2 - x - 2) / (x -1)^2
Bài 4: Đường tiệm cận
Giải bài 48 trang 24 SBT Giải tích 12 Bài 4: Đường tiệm cận của hàm số giúp học sinh biết cách làm bài tập trong SBT Toán 12.
Bài 1.48 trang 24 Sách bài tập Giải tích 12: Tìm các tiệm cận đứng và ngang của đồ thị mỗi hàm số sau:
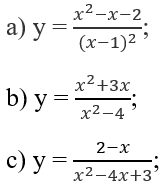
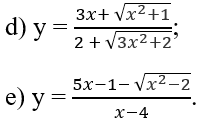
Lời giải:
a) Vì
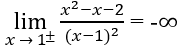
nên x = 1 là tiệm cận đứng.
Từ
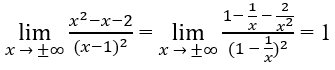
Suy ra y = 1 là tiệm cận ngang.
b) Vì
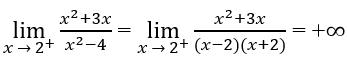
và
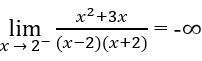
nên x = 2 là một tiệm cận đứng.
Do
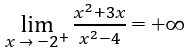
và
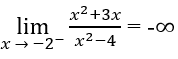
nên x = -2 là tiệm cận đứng thứ hai.
Ta lại có
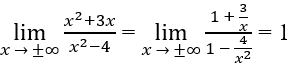
nên y = a là tiệm cận ngang.
c) Do
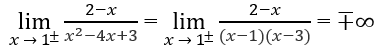
nên x = 1 là tiệm cận đứng.
Mặt khác,
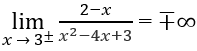
nên x = 3 cũng là tiệm cận đứng.
Vì
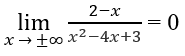
nên y = 0 là tiệm cận ngang.
d) TXĐ: R.
Từ
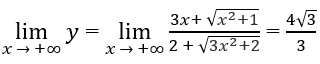
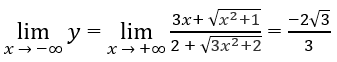
Ruy ra đồ thị hàm số có các tiệm cận ngang:
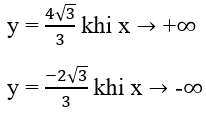
Đồ thị hàm số không có tiệm cận đứng.
e) TXĐ: D = (-∞; -√2) ∪ (√2;4) ∪ (4; +∞)
Do
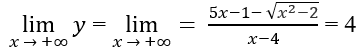
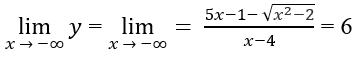
Cho nên đồ thị hàm số có hai tiệm cận ngang
y = 4 khi x ⇒ +∞
y = 6 khi x ⇒ -∞
Vì
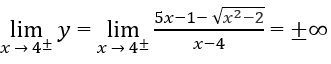
Cho nên đường thẳng x = 4 là tiệm cận đứng của đồ thị hàm số.

