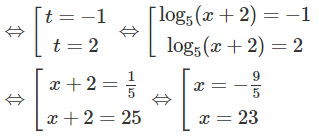Bài 2.49 trang 125 Sách bài tập Giải tích 12

Bài 5: Phương trình mũ và phương trình lôgarit

Bài 2.49 trang 125 Sách bài tập Giải tích 12:

Lời giải:

a) log₂(2^x + 1) .log₂ [2(2^x + 1)] = 2

⇔ log₂ (2^x + 1). [1 + log₂ (2^x + 1)] = 2

Đặt t = log₂ (2^x + 1), ta có phương trình

t(1 + t) = 2 ⇔ t² + t – 2 = 0

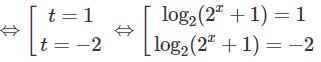
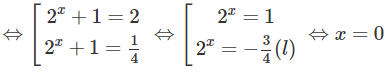
b) Với điều kiện x >0, ta có: log(x^log9) = log(9^logx)

log(x^log9) = log9.logx và log(9^logx) = logx.log9

Nên log(x^log9) = log(9^logx)

Suy ra: x^log9 = 9^logx

Đặt t = x^log9, ta được phương trình 2t = 6 ⇔ t = 3 ⇔ x^log9 = 3

⇔ log(x^log9) = log3

⇔log9.logx = log3

⇔logx = log3/log9 ⇔ logx = 1/2

⇔ x = √10 (thỏa mãn điều kiện x > 0)

c) Với điều kiện x > 0, lấy logarit thập phân hai vế của phương trình đã cho, ta được:

(3log³x − 2logx/3).logx = 7/3

Đặt t = logx, ta được phương trình 3t⁴ − 2t²/3 – 7/3 = 0

⇔ 9t⁴ − 2t² − 7 = 0

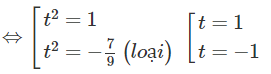
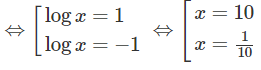
d) Đặt t = log₅(x + 2) với điều kiện x + 2 > 0, x + 2 ≠ 1, ta có:

1 + 2/t = t ⇔ t² – t – 2 = 0 , t ≠ 0