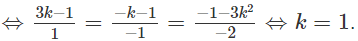Trong không gian Oxyz, cho hai mặt phẳng (β) : x + 3ky – z + 2 = 0 và (γ) : kx – y + z + 1 = 0

Đề toán tổng hợp chương 3

Bài 3.64 trang 134 Sách bài tập Hình học 12: Trong không gian Oxyz, cho hai mặt phẳng (β) : x + 3ky – z + 2 = 0 và (γ) : kx – y + z + 1 = 0

Tìm k để giao tuyến của (β) và (γ) vuông góc với mặt phẳng

(α): x – y – 2z + 5 = 0.

Lời giải:

Ta có n_β→ = (1; 3k; −1) và n_γ→ = (k; −1; 1). Gọi d_k = β ∩ γ

Đường thẳng dk vuông góc với giá của n_β→ và n_γ→ nên có vecto chỉ phương là: a→ = _β→ ∧ n_γ→ = (3k − 1; −k − 1; −1 − 3k²)

Ta có: d_k ⊥ (α)