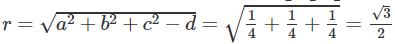Trong không gian Oxyz, cho bốn điểm A(1; 0; 0), B(0; 1; 0), C(0; 0; 1) và D(1; 1; 0). Viết phương trình mặt cầu (S)

Đề toán tổng hợp chương 3

Bài 3.67 trang 135 Sách bài tập Hình học 12: Trong không gian Oxyz, cho bốn điểm A(1; 0; 0), B(0; 1; 0), C(0; 0; 1) và D(1; 1; 0).

a) Viết phương trình mặt cầu (S) đi qua bốn điểm A, B, C, D.

b) Xác định tọa độ tâm và bán kính của đường tròn là giao tuyến của mặt cầu (S) với mặt phẳng (ACD).

Lời giải:

a) Phương trình mặt cầu (S) có dạng x² + y² + z² – 2ax – 2by – 2cz + d = 0 (*)

Thay tọa độ các điểm A, B, C, D vào (*) ta có:

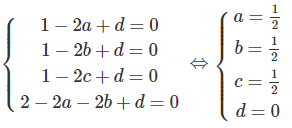
Vậy phương trình mặt cầu (S) là: x² + y² + z² – x – y – z = 0

b) Ta có AC→ = (−1; 0; 1) và AD→ = (0; 1; 0)

Suy ra (ACD) có vecto pháp tuyến n→ = AC→ ∧ AD→ = (−1; 0; −1) hay n'→ = (1; 0; 1)

Vậy phương trình của mặt phẳng (ACD) là x – 1 + z = 0 hay x + z – 1 = 0

Mặt cầu (S) có tâm

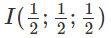
Ta có I ∈ (ACD), suy ra mặt phẳng (ACD) cắt (S) theo một đường tròn có tâm và có bán kính r bằng bán kính mặt cầu (S)

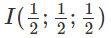
vậy: