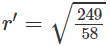Cho mặt phẳng (P): 2x – 3y + 4z – 5 = 0 và mặt cầu (S): x^2 + y^2 + z^2 + 3x + 4y – 5z + 6 = 0

Đề toán tổng hợp chương 3

Bài 3.65 trang 134 Sách bài tập Hình học 12: Cho mặt phẳng (P): 2x – 3y + 4z – 5 = 0 và mặt cầu (S):

x² + y² + z² + 3x + 4y – 5z + 6 = 0

a) Xác định tọa độ tâm I và bán kính r của mặt cầu (S).

b) Tính khoảng cách từ tâm I đến mặt phẳng (P). Từ đó chứng minh rằng mặt phẳng (P) cắt mặt cầu (S) theo một đường tròn mà ta kí hiệu là (C). Xác định bán kính r’ và tâm H của đường tròn (C) .

Lời giải:

a) (S) có tâm

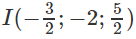
và có bán kính

b)

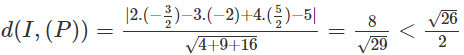
Vậy d(I, (P)) < r

Suy ra mặt phẳng (P) cắt mặt cầu (S) theo đường tròn tâm H bán kính r’.

H chính là hình chiếu vuông góc của I xuống mặt phẳng (P). Gọi Δ là đường thẳng qua I và vuông góc với (P). Ta có vecto chỉ phương của Δ là

a_Δ→ = n_(P)→ = (2; −3; 4)

Phương trình tham số của Δ:

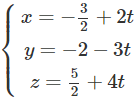
Δ cắt (P) tại

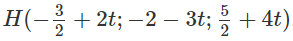
Ta có: H ∈ (α)

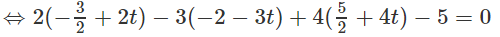
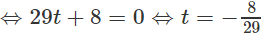
Suy ra tọa độ

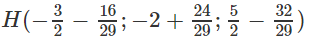
Ta có

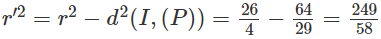
Suy ra