Tìm giá trị lớn nhất và nhỏ nhất của các hàm số sau trên các khoảng, đoạn tương ứng

Ôn tập cuối năm

Bài 7 trang 216 Sách bài tập Giải tích 12: Tìm giá trị lớn nhất và nhỏ nhất của các hàm số sau trên các khoảng, đoạn tương ứng:

a) g(x) = |x3 + 3x2 – 72x + 90| trên đoạn [-5; 5]

b) f(x) = x4 – 4x2 + 1 trên đoạn [-1; 2]

c) f(x) = x – ln x + 3 trên khoảng (0; ∞)

Lời giải:

a) Xét hàm số f(x) = x3 + 3x2 − 72x + 90 trên đoạn [-5;5]

f′(x) =3x2 + 6x − 72;

f′(x) = 0

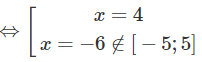
f(−5) = 400; f(5) = −70; f(4) = −86

Ngoài ra, f(x) liên tục trên đoạn [-5;5] và f(−5).f(5) < 0 nên tồn tại x₀ ∈ (−5;5) sao cho f(x₀) = 0

Ta có g(x) = |f(x)| ≤ 0 và g(x₀) = |f(x₀)| = 0;

g(−5) = |400| = 400

g(5) = |−70| = 70; g(4) = |f(4)| = |−86| = 86

Vậy min g(x) = g(x₀) = 0; max g(x) = g(−5) = 400

b) min f(x) = f(√2) = −3; max f(x) = f(2) = f(0) = 1

c) min f(x) = f(1) = 4. Không có giá trị lớn nhất.