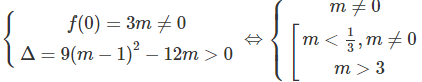Cho hàm số. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1) khi m = 0

Ôn tập cuối năm

Bài 8 trang 217 Sách bài tập Giải tích 12: Cho hàm số:

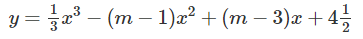
(m là tham số) (1)

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1) khi m = 0.

b) Viết phương trình của tiếp tuyến với đồ thị (C) tại điểm A(0; 9/2)

c) Tính diện tích hình phẳng giới hạn bởi (C) , trục hoành và các đường thẳng x = 0 và x = 2.

d) Xác định m để đồ thị của (1) cắt đường thẳng y = −3x + 9/2 tại ba điểm phân biệt.

Lời giải:

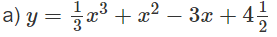
    +) Tập xác định: D = R

    +) Sự biến thiên: y’ = x² + 2x – 3

y' = 0

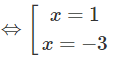
Bảng biến thiên:

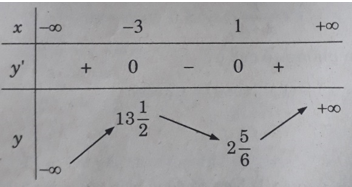
Hàm số đồng biến trên các khoảng (-∞; -3) và (1; +∞), nghịch biến trên khoảng (-3; 1).

Hàm số đạt cực đại tại x = −3; y_CD = 27/2; y_CT = 17/6 khi x = 1

Đồ thị cắt trục tung tại điểm (0; 9/2) và có dạng như hình dưới đây.

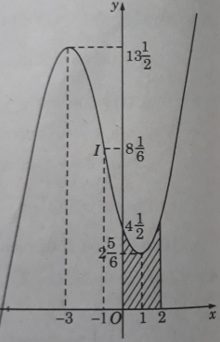
y′′ = 2x + 2; y′′ = 0 ⇔ x = −1. Vậy là tâm đối xứng của đồ thị.

b) Tiếp tuyến với (C) đi qua A(0; 9/2) có phương trình là: y = f′(0)x + 9/2, trong đó f(x) = x³/3 + x² − 3x + 9/2

Ta có f ’(0) = -3.

Vậy phương trình tiếp tuyến là y = −3x + 9/2

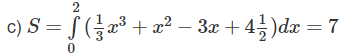
d) Hoành độ giao điểm của đường thẳng y = −3x + 9/2 với đồ thị của (1) thỏa mãn phương trình

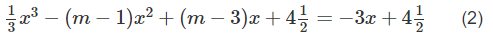
Ta có (2) ⇔ x³/3 − (m − 1)x² + mx = 0 (2)

⇔ x[x² − 3(m − 1)x + 3m] = 0

Để (2) có ba nghiệm phân biệt thì phương trình f(x) = x²– 3(m – 1)x + 3m = 0 phải có hai nghiệm phân biệt khác 0, tức là: