Giải các bất phương trình sau: (2x − 7)ln(x + 1) > 0; (x − 5)(logx + 1) < 0;

Bài tập ôn tập chương 2

Bài 2.72 trang 134 Sách bài tập Giải tích 12: Giải các bất phương trình sau:

a) (2x − 7)ln(x + 1) > 0;

b) (x − 5)(logx + 1) < 0;

c) 2log₃²x + 5log₂² + log₂x – 2 ≥ 0

d) ln(3e^x − 2) ≤ 2x

Lời giải:

a) Bất phương trình đã cho tương đương với hệ sau:

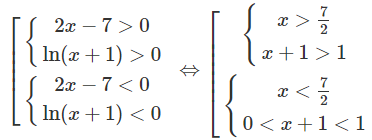
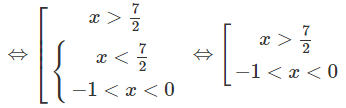
Vậy tập nghiệm là (−1;0) ∪ (7/2; +∞)

b) Tươngg tự câu a), tập nghiệm là (1/10; 5)

c) Đặt t = log₂x, ta có bất phương trình 2t³ + 5t² + t – 2 ≥ 0 hay (t + 2)(2t² + t − 1) ≥ 0 có nghiệm −2 ≤ t ≤ −1 hoặc t ≥ 1/2

Suy ra 1/4 ≤ x ≤ 1/2 hoặc x ≥ √2

Vậy tập nghiệm của bất phương trình đã cho là: [1/4; 1/2] ∪ [√2; +∞)

d) Bất phương trình đã cho tương đương với hệ:

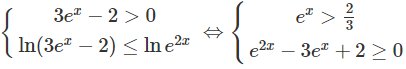
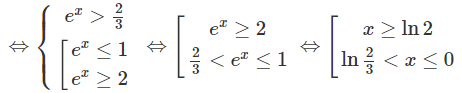
Vậy tập nghiệm là (ln(2/3); 0] ∪ [ln2; +∞)