Trong không gian cho ba vecto tùy ý. Bài 3.8 trang 103 Sách bài tập Hình học 12

Bài 1: Hệ tọa độ trong không gian

Bài 3.8 trang 103 Sách bài tập Hình học 12: Trong không gian cho ba vecto tùy ý a→, b→, c→.

Gọi u→ = a→ − 2b→, v→ = 3b→ − c→, w→ = 2 c→ − 3a→.

Chứng tỏ rằng ba vecto u→, v→, w→ đồng phẳng.

Lời giải:

Muốn chứng tỏ rằng ba vecto u→, v→, w→ đồng phẳng ta cần tìm hai số thực p và q sao cho w→ = pu→ + qv→.

Giả sử có w→ = pu→ + qv→

2c→ – 3a→ = p(a→ – 2b→) + q(3b→ − c→)

⇔ (3 + p)a→ + (3q − 2p)b→ − (q + 2)c→ =0→ (1)

Vì ba vecto lấy tùy ý a→, b→, c→ nên đẳng thức (1) xảy ra khi và chỉ khi:

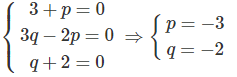
Như vậy ta có: w→ = −3u→ − 2v→ nên ba vecto u→, v→, w→ đồng phẳng.