Trong không gian Oxyz cho một vecto. Bài 3.9 trang 104 Sách bài tập Hình học 12
Bài 1: Hệ tọa độ trong không gian
Bài 3.9 trang 104 Sách bài tập Hình học 12: Trong không gian Oxyz cho một vecto a→ tùy ý khác vecto 0→. Gọi α, β, γ là ba góc tạo bởi ba vecto đơn vị i→, j→, k→ trên ba trục Ox, Oy, Oz và vecto a→. Chứng minh rằng: cos2α + cos2β + cos2γ = 1
Lời giải:
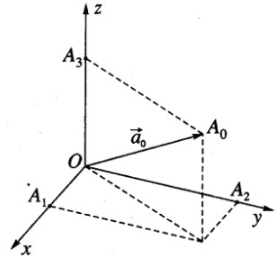
Gọi a0→ là vecto đơn vị cùng hướng với vecto a→
ta có
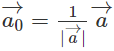
GọiOA0→ = a0→ và các điểm A1, A2, A3 theo thứ tự là hình chiếu vuông góc của điểm A0 trên các trục Ox, Oy, Oz.
Khi đó ta có:
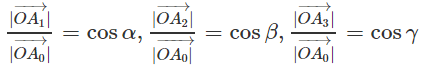
Vì
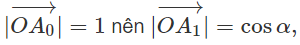
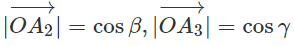
Ta có:
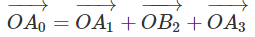
ta suy ra:
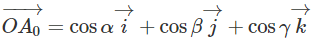
hay
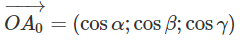
Vì OA0→ = a0→ mà |a0→ | = 1 nên ta có: cos2α + cos2β + cos2γ = 1

