Bài 139, 140, 141 trang 34 SBT Toán 7 tập 1

Bài 139, 140, 141 trang 34 SBT Toán 7 tập 1

Bài 139:

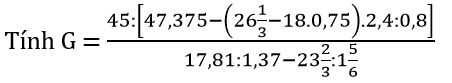
Lời giải:

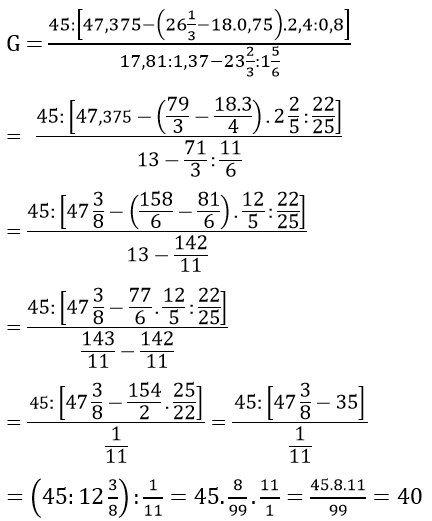
Bài 140: Cho x, y ∈ Q. Chứng tỏ rằng

a) |x + y| ≤ |x| + |y|.

b) |x - y| ≥ |x| - |y|.

Lời giải:

a) Với mọi x, y ∈ Q ta luôn có x ≤ |x| và -x ≤ |x|;

y ≤ |y| và -y ≤ |y| ⇒ x + y ≤ |x| + |y| và -x – y ≤ |x| + |y|

hay x + y ≥ -(|x| + |y|).

Do đó –(|x| + |y|) ≤ x + y ≤ |x| + |y|.

Vậy |x + y| ≤ |x| + |y|.

(Dấu “=” xảy ra khi xy ≥ 0.

b) Theo câu a ta có: |x - y| + |y| ≥ |x – y + y| = |x| ⇒ |x - y| ≥ |x| - |y|.

Bài 141: Tìm giá trị nhỏ nhất của biểu thức:

A = |x – 2001| + |x -1|

Lời giải:

Vì |1 - x| = |x - 1| nên A = |x - 2001| + |x - 1|

= |x - 2001| + |1 - x| ≥ | x – 2001 + 1 - x| = 2000

Vậy giá trị nhỏ nhất của biểu thức A = 2000 khi x – 2001 và 1 – x cùng dấu

Vậy 1 ≤ x ≤ 2001