Bài 47, 48, 49 trang 114 SBT Toán 7 tập 1

Bài 47, 48, 49 trang 114 SBT Toán 7 tập 1

Bài 47: Vẽ hình theo trình tự sau:

- Vẽ tam giác Abc

- Vẽ đường thẳng đi qua A vuông goác với BC tại H

- Vẽ đường thẳng đi qua H vuông góc với AC tại T

- Vẽ đường thẳng đi qua T song song với BC

Trong các hình a,b,c,d dưới đây thì những hình nào vẽ đúng đề bài trên, hãy điền tên các điểm (theo đề bài) cho các hình vẽ đúng.

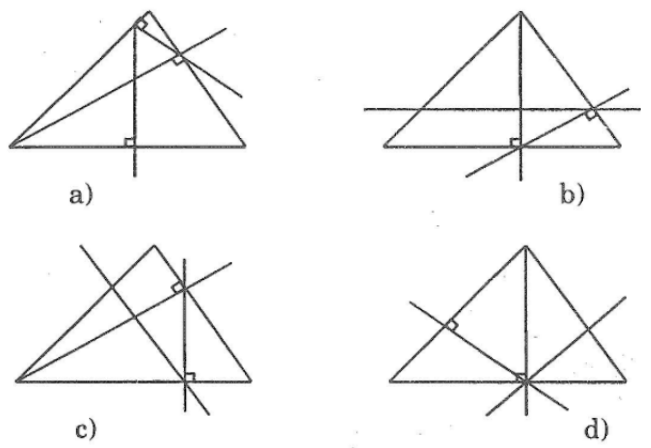
Lời giải:

Hình a sai ; Hình b đúng ; Hình c đúng ; Hình d sai

Tên các điểm được thể hiện trong hình dưới:

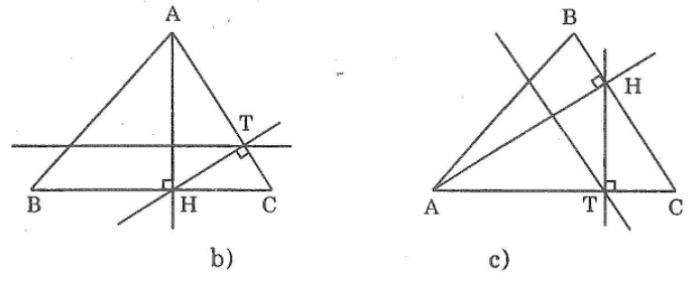
Bài 48: Hình dưới cho biết ∠A = 140°; ∠B = 70°; ∠C = 150°

Chứng minh rằng Ax //Cy

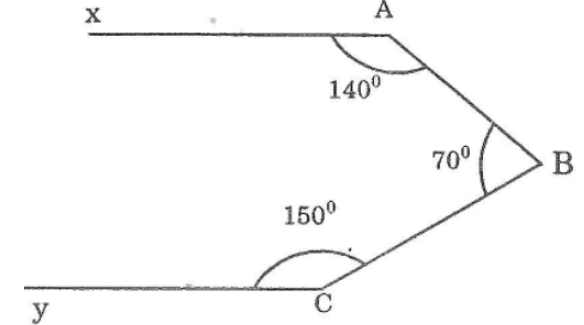
Lời giải:

Kẻ tia Bz // Ax và Cy’ là tia đối của tia Cy.

Ta có: ∠(B₂ ) +∠(xAB) = 180°

(hai góc trong cùng phía)

Mà ∠(xAB) = 140°(gt)

Suy ra: ∠(B₂ ) =180 - ∠(xAB) = 180° - 140° = 40°

Mà: ∠(B₁ ) +∠(B₂ ) =∠(ABC) (B₁ ) = ∠(ABC) -(B₂ ) = 70° - 40° = 30°     (1)

∠(yCB) +∠(BCy') = 180°(2 góc kề bù)

∠BCy' = 180° - ∠(yCB) = 180° - 150° = 30°     (2)

Từ (1) và (2) ta có: ∠(B₁ ) =∠(BCy')

Suy ra: Cy’ // Bz ( vì có cặp góc ở vị trí so le trong bằng nhau)

Hay Cy // Bz mà Bz // Ax suy ra Ax // Cy

Bài 49: Hình dưới đây cho biết ∠A +∠B + ∠C = 360°. Chứng minh rằng Ax // Cy

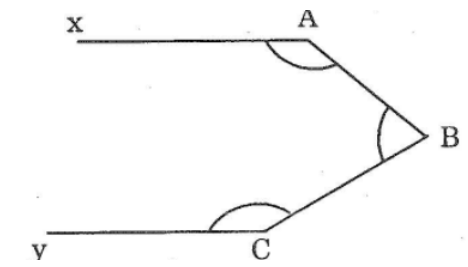
Lời giải:

Kẻ Bz // Ax và Cy’ là tia đối của tia Cy

Ta có: ∠A +∠(B₂ ) = 180°

(2 góc trong cùng phía)     (1)

∠A + ∠B + C = 360° (gt)

∠A + ∠(B₂ ) +∠(B₁ ) +∠C = 360°     (2)

Từ (1)và (2)suy ra :

∠(B₁) + ∠C = 180°     (3)

∠(C₁ ) + ∠∠C = 180° (hai góc kề bù)     (4)

Từ (3) và (4) suy ra: ∠(B₁ ) = ∠(C₁ )

Suy ra: Cy’ // Bz (vì có cặp góc so le trong bằng nhau)

Hay Cy // Bz mà Bz // Ax suy ra : Ax // Cy