Bài 2.1, 2.2, 2.3 trang 82 SBT Toán 8 tập 1

Bài 2.1 trang 82 SBT Toán 8 Tập 1: Hình thang ABCD (BC// AD) có ∠C = 3∠D. Khẳng định nào dưới đây là đúng ?

A. ∠(A ) = 45^o

B. ∠(B ) = 45^o

C. ∠(C ) = 45^o

D. ∠(D ) = 60^o

Lời giải:

Chọn C. (D ) = 45^o

Bài 2.2 trang 82 SBT Toán 8 Tập 1: Hình thang ABCD (AB // CD) có ∠A - ∠D = 40^o, ∠A = 2∠C . Tính các góc của hình thang

Lời giải:

Hình thang ABCD có AB // CD

⇒ có ∠A + ∠D = 180^o (hai góc trong cùng phía bù nhau)

∠A - ∠D = 40^o (gt)

⇒ 2∠A = 220^o ⇒ ∠A = 110^o

∠D = ∠A - 40^o = 110^o – 40^o = 70^o

∠A = 2∠C (gt)

⇒ ∠C = ∠A /2 = 110^o : 2 = 55^o

∠B + ∠C = 180^o (hai góc trong cùng phía bù nhau)

⇒B = 180^o- ∠C = 180^o – 55^o = 125^o

Bài 2.3 trang 82 SBT Toán 8 Tập 1: Cho tam giác ABC vuông cân tại A, BC = 2 cm. Ở phía ngoài tam giác ABC, vẽ tam giác ACE vuông cân tại E.

a. Chứng minh rằng AECB là hình thang vuông

b. Tính các góc và các cạnh của hình thang AECB

Lời giải:

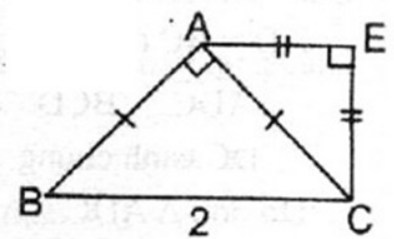
a. Tam giác ABC vuông cân tại A

⇒ ∠(ACB) = 45^o

Tam giác EAC vuông cân tại E

⇒ ∠(EAC) = 45^o

Suy ra: ∠(ACB) = ∠(EAC)

⇒ AE // BC (vì có cặp góc ở vị trí so le trong bằng nhau)

nên tứ giác AECB là hình thang có ∠E = 90^o. Vậy AECB là hình thang vuông

b) ∠E = ∠(ECB) = 90^o, ∠B = 45^o

∠B + ∠(EAB) = 180^o (hai góc trong cùng phía bù nhau)

⇒ ∠(EAB) = 180^o - ∠B = 180^o – 45^o = 135^o

Tam giác ABC vuông tại A. Theo định lí Py-ta-go ta có:

AB² + AC² = BC² mà AB = AC (gt)

⇒ 2AB²= BC² = 2² = 4

AB² = 2 ⇒ AB= √2(cm) ⇒ AC = √2 (cm)

Tam giác AEC vuông tại E. Theo định lí Py-ta-go ta có:

EA² + EC² = AC², mà EA = EC (gt)

⇒ 2EA² = AC² = 2

EA² = 1

⇒ EA = 1(cm) ⇒ EC = 1(cm)