Bài 18, 19, 20, 21 trang 82 SBT Toán 8 tập 1
Haylamdo giới thiệu lời giải bài tập Toán 8 Bài 18 đầy đủ sgk, sbt Kết nối tri thức sẽ giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 Bài 18.
(SGK + SBT) Toán 8 Bài 18 (sách mới) | Kết nối tri thức
- Giải sgk Toán 8 Bài 18 (sách mới):
- Giải sbt Toán 8 Bài 18 (sách mới):
Lưu trữ: Giải SBT Toán 8 Bài 18 trang 82 SBT Toán 8 Tập 1 (sách cũ)
Bài 18 trang 82 SBT Toán 8 Tập 1: Cho tam giác ABC vuông cân tại A. Ở phía ngoài tam giác ABC, ve tam giác BCD vuông cân tại B. Tứ giác ABCD là hình gì? Vì sao?
Lời giải:
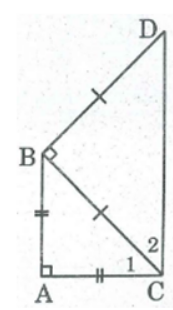
Vì ΔABC vuông cân tại A nên ∠C1= 45o
Vì ΔBCD vuông cân tại B nên ∠C2= 45o
∠(ACD) = ∠C1+ ∠C2= 45o + 45o = 90o
⇒ AC ⊥ CD
Mà AC ⊥ AB (gt)
Suy ra: AB //CD
Vậy tứ giác ABCD là hình thang vuông.
Bài 19 trang 82 SBT Toán 8 Tập 1: Hình thang vuông ABCD có ∠A = ∠D = 90o, AB = AD = 2cm, DC = 4cm. Tính các góc của hình thang.
Lời giải:
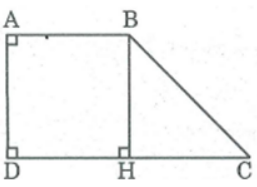
Kẻ BH ⊥ CD
Ta có: AD ⊥ CD (gt)
Suy ra: BH // AD
Hình thang ABHG có hai cạnh bên song song nên HD = AB và BH = AD
AB = AD = 2cm (gt)
⇒ BH = HD = 2cm
CH = CD – HD = 4 – 2 = 2 (cm)
Suy ra: ΔBHC vuông cân tại H ⇒ ∠C = 45o
∠B + ∠C = 180o (2 góc trong cùng phía) ⇒ ∠B = 180o – 45o = 135o
Bài 20 trang 82 SBT Toán 8 Tập 1: Chứng minh rằng tổng hai cạnh bên của hình thang lớn hơn hiệu của hai đáy.
Lời giải:
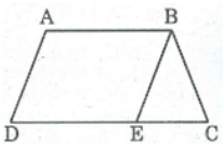
Giả sử hình thang ABCD có AB // CD
Từ B kẻ đường thẳng song song với AD cắt CD tại E.
Hình thang ABED có hai cạnh bên song song nên AB = ED và AD = BE
Ta có: CD – AB = CD – ED = EC (1)
Trong ΔBEC ta có:
BE + BC > EC (bất đẳng thức tam giác)
Mà BE = AD
Suy ra: AD + BC > EC (2)
Từ (1) và (2) suy ra: AD + BC > CD – AB
Bài 21 trang 82 SBT Toán 8 Tập 1: Trên hình vẽ dưới có bao nhiêu hình thang.
Lời giải:
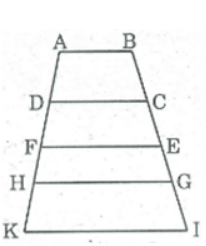
Trên hình vẽ có tất cả 10 hình thang.
Đó là: ABCD, ABEF, ABGH, ABIK, DCEF, DCGH, DCIK, FEGH, FEIK, HGIK

