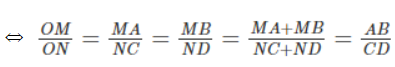(SGK + SBT) Giải Toán 8 trang 86 Kết nối tri thức, Chân trời sáng tạo
Haylamdo giới thiệu lời giải bài tập Toán 8 trang 86 Kết nối tri thức, Chân trời sáng tạo sẽ giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 trang 86.
(SGK + SBT) Giải Toán 8 trang 86 Kết nối tri thức, Chân trời sáng tạo
- Toán lớp 8 trang 86 Tập 1 (sách mới):
- Toán lớp 8 trang 86 Tập 2 (sách mới):
Lưu trữ: Giải SBT Toán 8 trang 86 (sách cũ)
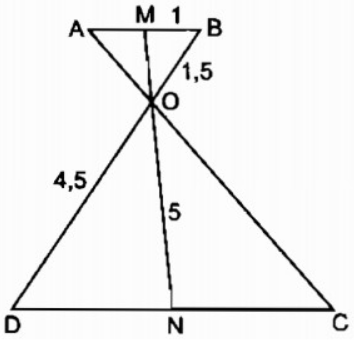
Bài 2.1 trang 86 sách bài tập Toán 8 Tập 2: Hình bs.1 cho biết AB // CD, O ∈ MN, MN = 5cm, OB = 1,5cm, OD = 4,5cm, MB = 1cm.
Hãy chọn kết quả đúng.
1. Độ dài của đoạn thẳng MO (tính theo đơn vị cm) là :
A. 1,25
B. 2,25
C. 3,25
D. 4,25
2. Độ dài của đoạn thẳng NO (tính theo đơn vị cm) là:
A. 5,75
B. 3,75
C. 4,25
D. 2,75
Lời giải:
1. Chọn A
2. Chọn C
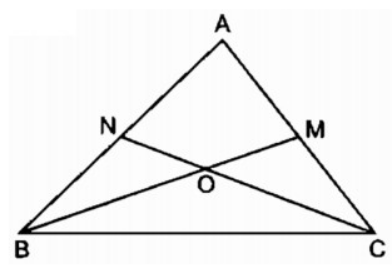
Bài 2.2 trang 86 sách bài tập Toán 8 Tập 2: Tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại O. Chứng minh rằng OM.OC = ON.OB
Lời giải:
Vì M, N lần lượt là trung điểm của cạnh AC và AB nên đường thẳng MN song song với BC.
Do đó tứ giác BCMN là hình thang và có hai đường chéo BM và CN cắt nhau tại O.
Theo kết quả chứng minh ở bài tập số 9, ta có: OM.OC = ON.OB.
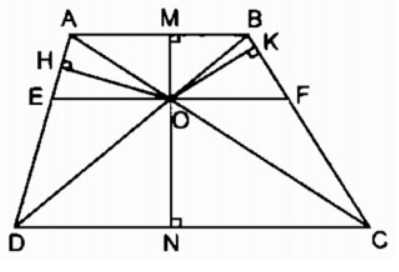
Bài 2.3 trang 86 sách bài tập Toán 8 Tập 2: Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O. Gọi M, K, N, H lần lượt là chân đường vuông góc hạ từ O xuống các cạnh AB, BC, CD, DA. Chứng minh rằng:
Lời giải:
a. Vì OM ⊥ AB và ON ⊥ CD, mà AB // CD nên suy ra M, O, N thẳng hàng.
Mặt khác, do AB // CD nên theo Định lí Ta-lét ta có:
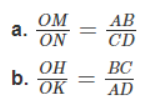
Từ đó, theo tính chất của dãy tỉ số bằng nhau, ta có:
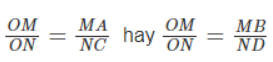
b. Từ O kẻ đường thẳng song song với AB và CD cắt AD tại E, cắt BC tại F.
Áp dụng kết quả chứng minh ở bài 14 ta có:
OE = OF
Từ đó, ta có:
SAEO = SBFO (1) (hai tam giác có cùng đường cao và hai đáy bằng nhau);
SDEO = SCFO (2)
Từ (1) và (2) suy ra : SOAD = SOBC (3)
Suy ra: OH.AD = OK.BC