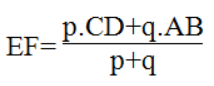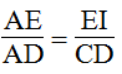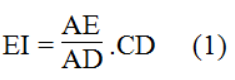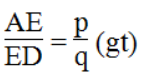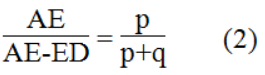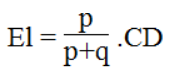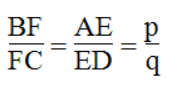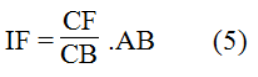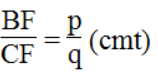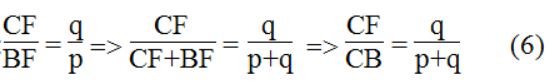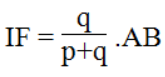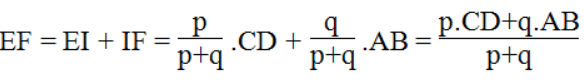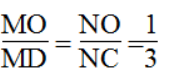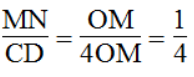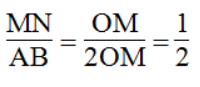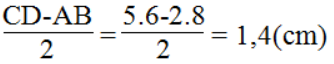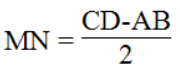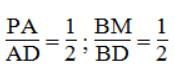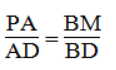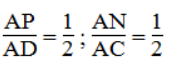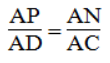(SGK + SBT) Giải Toán 8 trang 85 Kết nối tri thức, Chân trời sáng tạo, Cánh diều
Haylamdo giới thiệu lời giải bài tập Toán 8 trang 85 Kết nối tri thức, Chân trời sáng tạo, Cánh diều sẽ giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 trang 85.
(SGK + SBT) Giải Toán 8 trang 85 Kết nối tri thức, Chân trời sáng tạo, Cánh diều
- Toán lớp 8 trang 85 Tập 1 (sách mới):
- Toán lớp 8 trang 85 Tập 2 (sách mới):
Lưu trữ: Giải SBT Toán 8 trang 85 (sách cũ)
Bài 11 trang 85 sách bài tập Toán 8 Tập 2: Cho hình thang ABCD (AB // CD). Trên cạnh AD lấy điểm E sao cho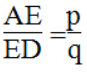 
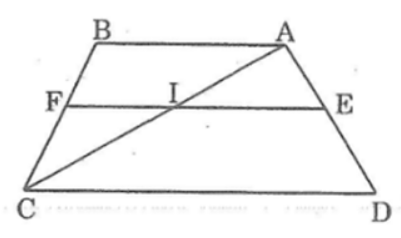
.Qua E kẻ đường thẳng song song với các đáy và cắt BC tại F. Chứng minh rằng: 
Lời giải:
Kẻ đường chéo AC cắt EF tại I
Trong ΔAEC, ta có: EI // CD
Suy ra: 
Suy ra: 
Lại có : 
Suy ra: 
Từ (1) và (2) suy ra: 
Trong ΔABC, ta có: IE // AB
Suy ra: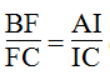 
(định lí ta-lét) (3)
Trong ΔADC, ta có : EI // CD
Suy ra: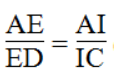 
(định lí ta-lét) (4)
Từ (3) và (4) suy ra 
Trong ΔABC, ta có: IF // BC
Suy ra: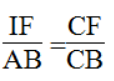 
(định lí ta-lét)
Suy ra: 
Ta có: 
Suy ra: 
Từ (5) và (6) suy ra: 
Vậy: 
Bài 12 trang 85 sách bài tập Toán 8 Tập 2: Hình thang cân ABCD (AB//CD) có hai đường chéo AC và BD cắt nhau tại O. Gọi M, N theo thứ tự là trung điểm của BD và AC. Cho biết MD = 3MO, đáy lớn CD = 5,6cm
a. Tính độ dài đoạn thẳng MN và đáy nhỏ AB.
b.So sánh độ dài đoạn thẳng MN với nửa hiệu của CD và AB
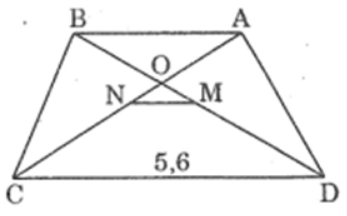
Lời giải:
a. Vì ABCD là hình thang cân có AB // CD nên:
AC = BD (1)
Xét ΔADC và ΔBCD, ta có:
AC = BD (chứng minh trên)
AD = BC (ABCD cân)
CD cạnh chung
Suy ra: ΔADC = ΔBCD (c.c.c)
Suy ra : ∠(ACD) =∠( BDC)
Hay ∠(OCD) = ∠( ODC)
Suy ra tam giác OCD cân tại O
Suy ra: OD = OC (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: OA = OB
Lại có: MD = 3MO (gt) ⇒ NC = 3NO
Trong ΔOCD, ta có: 
Suy ra: MN // CD (Định lí đảo của định lí Ta-lét)
Ta có: OD = OM + MD = OM + 3OM = 4OM
Trong ΔOCD, ta có: MN // CD
Suy ra: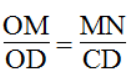 
Hệ quả định lí Ta-lét)
Suy ra: 
Suy ra: MN = 1/4 CD = 1/4 .5,6 = 1,4 (cm)
Ta có: MB = MD (gt)
Suy ra: MB = 3OM hay OB = 2OM
Lại có: AB // CD (gt) suy ra: MN // AB
Trong ΔOAB, ta có: MN // AB
Suy ra: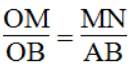 
(Hệ quả định lí Ta-lét)
Suy ra: 
Vậy: AB = 2MN = 2.1,4 = 2,8(cm)
b.Ta có: 
Vậy 
Bài 13 trang 85 sách bài tập Toán 8 Tập 2: Cho hình thang ABCD (AB // CD, AB < CD). Gọi trung điểm các đường chéo AC, BD thứ tự là N và M. Chứng minh rằng:
a. MN // AB
b. MN = (CD-AB)/2
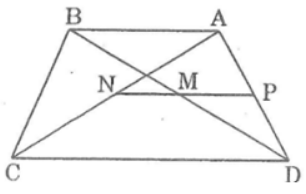
Lời giải:
a. Gọi P là trung điểm của AD, nối PM
Trong ΔDAB ta có: 
Suy ra: 
Suy ra: PM // AB (Định lí đảo của định lí Ta-lét) (1)
Trong ΔACD, ta có 
Suy ra: 
Suy ra: PN // CD (định lí đảo định lí Ta-lét) (2)
Từ (1) và (2) và theo tiên đề Ơ-clít suy ra P, M, N thẳng hàng.
Vậy MN // CD hay MN // AB.
b. Vì PM là đường trung bình của tam giác DAB nên:
PM = AB/2 (tính chất đường trung bình tam giác)
Vì PN là đường trung bình của tam giác ΔACD nên:
PN = CD/2 (tính chất đường trung hình tam giác)
Mà PN = PM + MN
Suy ra: MN = PN – PM = CD/2 - AB/2 = (CD-AB)/2
Bài 14 trang 85 sách bài tập Toán 8 Tập 2: Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M, N. Chứng minh rằng OM = ON.
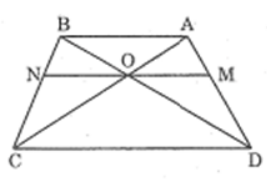
Lời giải:
Trong ΔDAB, ta có: OM // AB (gt)
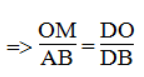(Hệ quả định lí Ta-lét) (1)
Trong ΔCAB, ta có: ON // AB (gt)
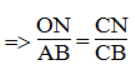(Hệ quả định lí Ta-lét) (2)
Trong ΔBCD, ta có: ON // CD (gt)
Suy ra: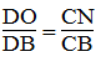 
(định lí Ta-lét) (3)
Từ (1), (2) và (3) suy ra: 
Vậy: OM = ON
