Bài 12.1, 12.2, 12.3 trang 99 SBT Toán 8 tập 1

---

Bài 12.1, 12.2, 12.3 trang 99 SBT Toán 8 tập 1

Bài 12.1 trang 99 SBT Toán 8 Tập 1: Hình vuông có chu vi bằng 8 thì đường chéo bằng :

A. 2

B. √32

C. √8

D. √2

Hãy chọn phương án đúng.

Lời giải:

Chọn C. √8 Đúng

Bài 12.2 trang 99 SBT Toán 8 Tập 1: Cho hình thoi ABCD, O là giao điểm của hai đường chéo. Các tia phân giác của bốn góc vuông có đỉnh O cắt các cạnh AB, BC, CD, DA theo thứ tự ở E, F, G, H. Tứ giác EFGH là hình gì ?

Lời giải:

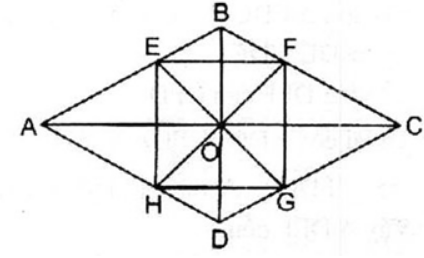
Ta có: ∠(AOB) và ∠(COD) đối đỉnh nên E, O, G thẳng hàng

∠(BOC) và ∠(AOD) đối đỉnh nên F, O, H thẳng hàng

Xét ΔBEO và ΔBFO:

∠(EBO) = ∠(FBO) (tính chất hình thoi)

OB cạnh chung

∠(EBO) = ∠(FBO) = 45^o (gt)

Do đó: ΔBEO = ΔBFO (g.c.g)

⇒ OE = OF (1)

Xét ΔBEO và ΔDGO:

∠(EBO) = ∠(GDO) (so le trong)

OB = OD(tính chất hình thoi)

∠(EOB) = ∠(GOD) (đối đỉnh)

Do đó: ΔBEO = ΔDGO (g.c.g)

⇒ OE = OG (2)

Xét ΔAEO và ΔAHO:

∠(EAO) = ∠(HAO) (tính chất hình thoi)

OA cạnh chung

∠(EOA) = ∠(HOA) = 45^o (gt)

Do đó: ΔAEO = ΔAHO (g.c.g)

⇒ OE = OH (3)

Từ (1), (2) và (3) suy ra: OE = OF = OG = OH hay EG = FH

nên tứ giác EFGH là hình chữ nhật (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường và bằng nhau)

OE ⊥ OF (tính chất hai góc kề bù)

hay EG ⊥ FH

Vậy hình chữ nhật EFGH là hình vuông.

Bài 12.3 trang 99 SBT Toán 8 Tập 1: Cho hình vuông ABCD. Trên cạnh DC lấy điểm E, trên cạnh BC lấy điểm F sao cho DE = CF. Chứng minh rằng AE = DF và AE ⊥ DF.

Lời giải:

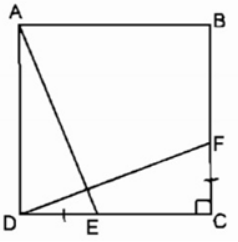
Xét ΔADE và ΔDCF:

AD = DC (gt)

∠A = ∠D = 90^o

DE = CF (gt)

Do đó: ΔADE = ΔDCF (c.g.c)

⇒ AE = DF

∠(EAD) = ∠(FDC)

∠(EAD) + ∠(DEA) = 90^o (vì ΔADE vuông tại A)

⇒∠(FDC) + ∠(DEA) = 90^o

Gọi I là giao điểm của AE và DF.

Suy ra: ∠(IDE) + ∠(DEI) = 90^o

Trong ΔDEI ta có: ∠(DIE) = 180^o – (∠(IDE) + ∠(DEI) ) = 180^o – 90^o = 90^o

Suy ra: AE ⊥ DF