Bài 1, 2 trang 183 SBT Toán 8 tập 2

---

Bài 1, 2 trang 183 SBT Toán 8 tập 2

Bài 1 trang 183 Sách bài tập Toán 8 Tập 2: Cho hình bình hành ABCD. O là giao điểm của hai đường chéo. Trên các cạnh AB, BC, CD, DA ta lần lượt lấy các điểm E, F, G, H sao cho AE = CG, BF = DH.

a) Xác định tâm đối xứng của hình bình hành ABCD.

b) Chứng minh EFGH là hình bình hành, tìm tâm đối xứng của nó.

c) O còn là tâm đối xứng của những hình bình hành nào?

Lời giải:

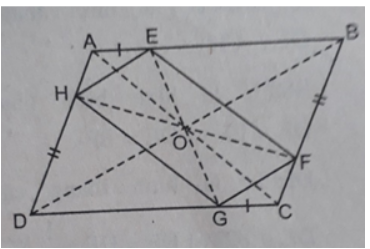
a) Tâm đối xứng của hình bình hành ABCD là giao điểm O của các đường chéo AC và BD.

b) AE//CG, AE = CG nên AECG là hình bình hành ⇒ O là trung điểm của EG. Tương tự O là trung điểm của HF.

Vậy O là tâm đối xứng của hình bình hành EFGH.

c) O còn là tâm đối xứng của các hình bình hành: AECG, EBGD, AHCF, DHBF.

Bài 2 trang 183 Sách bài tập Toán 8 Tập 2: Cho hình thang ABCD (AB // CD). Gọi M, N, P, Q theo thứ tự là trung điểm của AB, AC, CD, BD.

a) Chứng minh rằng MNPQ là hình bình hành.

b) Nếu ABCD là hình thang cân thì tứ giác MNPQ là hình gì? Vì sao?

c) Hình thang ABCD có thêm điều kiện gì thì MNPQ là hình vuông?

Lời giải:

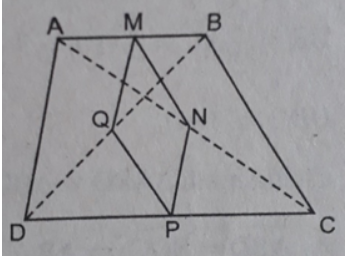
a) MN // QP (cùng song song với BC)

MN = QP ( =1/2 BC)

⇒ MNPQ là hình bình hành.

b) MNPQ là hình thoi vì là hình bình hành có hai cạnh kề bằng nhau.

c) Hình thang ABCD là hình thang cân có hai góc kề một đáy đều bằng 45^o thì MNPQ là hình vuông.