(SGK + SBT) Giải Toán 8 trang 96 Kết nối tri thức, Chân trời sáng tạo, Cánh diều
Haylamdo giới thiệu lời giải bài tập Toán 8 trang 96 Kết nối tri thức, Chân trời sáng tạo, Cánh diều sẽ giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 trang 96.
(SGK + SBT) Giải Toán 8 trang 96 Kết nối tri thức, Chân trời sáng tạo, Cánh diều
- Toán lớp 8 trang 96 Tập 1 (sách mới):
- Toán lớp 8 trang 96 Tập 2 (sách mới):
Lưu trữ: Giải SBT Toán 8 trang 96 (sách cũ)
Bài 126 trang 96 SBT Toán 8 Tập 1: Cho tam giác ABC, điểm M di chuyển trên cạnh BC. Gọi I là trung điểm của AM. Điểm I di chuyển trên đường nào?
Lời giải:
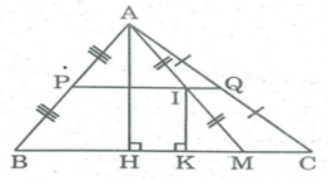
Kẻ AH ⊥ BC,IK ⊥ BC ⇒ AH // IK
Trong = ΔAHM, ta có:
AI = IM (gt)
IK // AH ( chứng minh trên)
Suy ra IK là đường trung bình của ΔAHM
⇒ IK = 1/2 AH
ΔABC cố định nên AH không thay đổi ⇒ IK = 1/2 AH không đổi.
I thay đổi cách BC một khoảng bằng AH/2 không đổi nên I nằm trên đường thẳng song song với BC, cách BC một khoảng bằng AH/2
Khi M trùng với điểm B thì I trùng với điểm P là trung điểm của AB.
Khi M trùng với điểm C thì I trùng với điểm Q là trung điểm của AC.
Vậy khi M di chuyển trên cạnh BC của ΔABC thì trung điểm I của AM chuyển động trên đường trung bình PQ của ΔABC
Bài 127 trang 96 SBT Toán 8 Tập 1: Cho tam giác ABC vuông tại A, điểm M thuộc cạnh BC. GỌi D,E theo thứ tự là chân đường vuông góc kẻ từ M đến AB, AC.
a. So sánh độ dài AM, DE.
b. Tìm vị trí của điểm M trên cạnh BC để DE có độ dài nhỏ nhất
Lời giải:
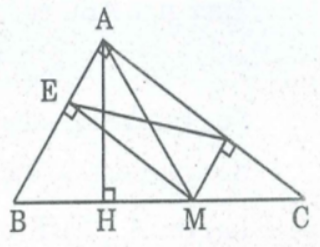
a. Xét tứ giác ADME, ta có:
∠A = 90o (gt)
MD ⊥ AB (gt)
⇒ ∠(MDA ) = 90o
ME ⊥ AC (gt)
⇒ ∠(MEA ) = 90o
Suy ra tứ giác ADME là hình chữ nhật ( vì có ba góc vuông)
⇒ AM = DE ( tính chất hình chữ nhật)
b. Ta có: AH ⊥ BC nên AM ≥ AH
Dấu “=” xảy ra khi M trùng với H
Mà DE = AM ( chứng minh trên)
Vậy DE có độ dài nhỏ nhất bằng AH khi M là chân đường vuông góc kẻ từ A đến BC
Bài 128 trang 96 SBT Toán 8 Tập 1: Cho điểm A nằm ngoài đường thẳng d. Điểm M di chuyển trên đường thẳng d. Gọi B là điểm đối xứng với A qua M. Điểm B di chuyển trên đường nào?
Lời giải:
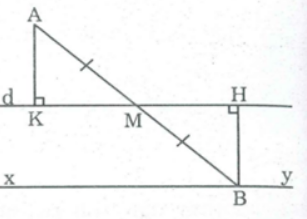
Kẻ AK ⊥ d,BH ⊥ d
Vì M thay đổi trên d, B đối xứng với A qua M nên AM = MB
Xét tam giác vuông AKM và BHM. Ta có: ∠(AKM ) = ∠(BHM ) = 90o
AM = MB ( chứng minh trên)
∠(AMK ) = ∠(BMH ) ( đối đỉnh)
Do đó ΔAKM = ΔAHM ( cạnh huyền,góc nhọn) ⇒ AK = BH
Điểm A cố định, đường thẳng d cố định nên AK không đổi.
M thay đổi, B thay đổi cách đường thẳng d cố định một khoảng bằng AK không thay đổi nên B chuyển động trên đường thẳng xy song song với d và cách d một khoảng bằng AK.
Bài 129 trang 96 SBT Toán 8 Tập 1: Cho đoạn thẳng AB, điểm M di chuyển trên đoạn thẳng ấy. Vẽ về một phía của AB các tam giác AMD, BME. Trung điểm I của DE di chuyển trên đường nào?
Lời giải:
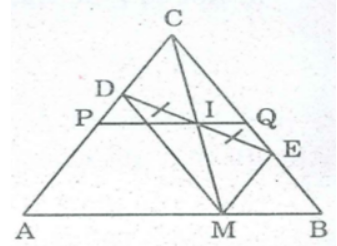
Gọi C là giao điểm của AD và BE.
Tam giác ABC có:
∠A = 60o (vì ΔADM đều)
∠B = 60o ( vì ΔBEM đều)
Suy ra: ΔABC đều hay AB = AC = BC
Suy ra điểm C cố định.
Lại có: ∠A = ∠(EMB ) = 60o
ME // AC ( vì có cặp góc đồng vị bằng nhau)
hay MD // EC
suy ra tứ giác CDME là hình bình hành.
I là trung điểm của DE nên I là trung điểm của CM
Kẻ CH ⊥ AB,IK ⊥ AB⇒IK // CH
Trong ΔCHM,ta có:CI = IM và IK // CH
Suy ra IK là đường trung bình của ΔCHM⇒IK = 1/2 CH
Vì C cố định nên CH không đổi ⇒ IK = 1/2 CH không đổi nên I chuyển động trên đường thẳng song óng với AB, cách AB một khoảng bằng 1/2 CH
Khi M trùng với A thì I trùng với trung điểm P của AC.
Khi M trùng với B thì I trùng với trung điểm Q của BC.
Vậy khi M chuyển động trên đoạn thẳng AB thì I chuyển động trên đoạn PQ ( P là trung điểm AC, Q là trung điểm BC).
Bài 130 trang 96 SBT Toán 8 Tập 1: Hình chữ nhật ABCD có cạnh AD bằng nửa đường chéo AC. Tính góc nhọn tạo bới hai đường chéo.
Lời giải:
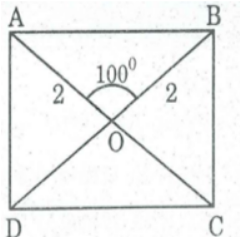
Gọi O là giao điểm của hai đường chéo AC và BD.
Ta có: AC = BD ( tính chất hình chữ nhật) ⇒ OA = OD = 1/2 AC
Lại có: AD = 1/2 AC (gt)
Suy ra: OA = OD = AD
⇒ ΔOAD đều ⇒∠(AOD ) = 60o
Bài 131 trang 96 SBT Toán 8 Tập 1: Dựng hình chữ nhật ABCD biết đường chéo AC = 4cm, góc tạo bởi hai đường chéo bằng 1000.
Lời giải:
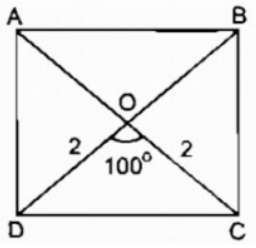
* Cách dựng:
- Dựng ΔOAB biết OA = OB = 2cm, ∠(AOB ) = 100o
- Trên tia đối tia OA dựng điểm C sao cho OC = OA = 2cm
- Trên tia đối tia OB dựng điểm D sao cho OD = OB = 2cm
Nối AD, BC, CD ta có hình chữ nhật ABCD cần dựng
* Chứng minh:
Ta có: OA = OC, OB = OD
Suy ra tứ giác ABCD là hình bình hành.
Vì AC = BD = 4 (cm) nên hình bình hành ABCD là hình chữ nhật.

