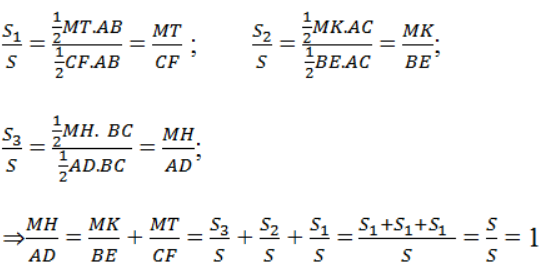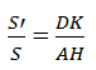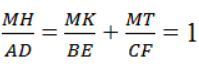Bài 3.2, 3.3 trang 161 SBT Toán 8 tập 1

---

Bài 3.2, 3.3 trang 161 SBT Toán 8 tập 1

Bài 3.2 trang 161 SBT Toán 8 Tập 1: Cho tam giác đều ABC và điểm M bất kì nằm trong tam giác đó. Đường thẳng đi qua điểm M và vuông góc với BC tại điểm H. Đường thẳng đi qua điểm M và vuông góc với CA tại điểm K. Đường thẳng đi qua điểm M và vuông góc với AB tại điểm T.

Lời giải:

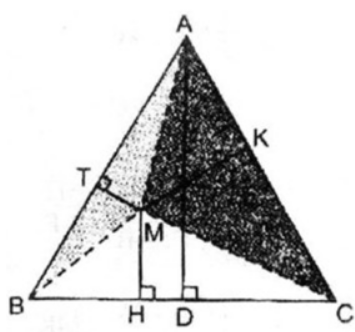
Giả sử ΔABC đều có cạnh bằng a, kẻ đường cao AD, đặt AD = h không đổi.

Ta có:

S_ABC = 1/2 ah

S_MAB = 1/2 MT.a

S_MAC = 1/2 MK.a

S_MBC = 1/2 MH.a

S_ABC = S_MAB + S_MAC + S_MBC

1/2 a.h = 1/2 MT.a + 1/2 MK.a + 1/2 MH.a

1/2 a. (MT + MK + MH)

⇒ MT + MK + MH = h không đổi

Vậy tổng MT + MK + MH không phụ thuộc vào điểm M.

Bài 3.3 trang 161 SBT Toán 8 Tập 1: a. Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC. Gọi S’ là diện tích của tam giác DBC.

Chứng minh rằng

b. Cho tam giác ABC và điểm M bất kì nằm trong tam giác đó. Kẻ các đường cao của tam giác đó là AD, BE và CF. Đường thẳng đi qua điểm M và song song với AD cắt cạnh BC tại điểm H. Đường thẳng đi qua điểm M và song song với BE cắt cạnh AC tại điểm K. Đường thẳng đi qua điểm M và song song với CF cắt cạnh BA tại điểm T.

Chứng minh rằng

Lời giải:

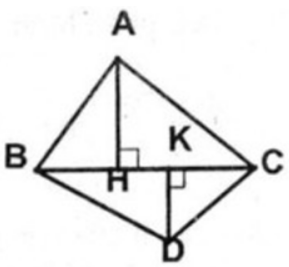
a. Hai ΔABC và ΔDBC có chung canh đáy BC nên ta có:

S_ABC = 1/2 AH. BC = S

S_DBC = 1/2 DK. BC = S'

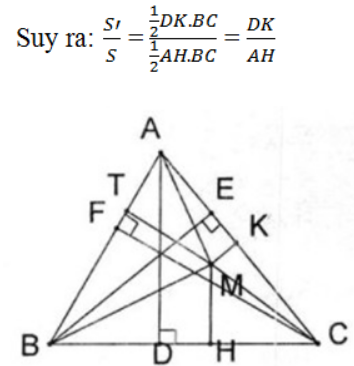
b. Gọi diện tích các hình tam giác ABC, MAB, MAC, MBC lần lượt là S, S₁, S₂, S₃. Ta có:

S = S₁ + S₂ + S₃

Trong đó: S = 1/2 AD.BC = 1/2 BE. AC = 1/2 CF. AB

S₁ = 1/2 MT. AB

S₂ = 1/2 MK. AC

S₃ = 1/2 MH. BC