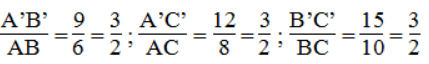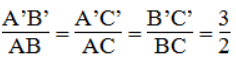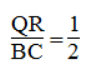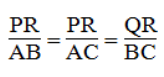Bài 29, 30, 31 trang 90 SBT Toán 8 tập 2

---

Bài 29, 30, 31 trang 90 SBT Toán 8 tập 2

Bài 29 trang 90 sách bài tập Toán 8 Tập 2: Hai tam giác mà các cạnh có độ dài như sau có đồng dạng không?

a. 4cm; 5cm; 6cm và 8mm; 10mm; 12mm.

b. 3cm; 4cm; 6cm và 9cm; 15cm; 18cm.

c. 1dm; 2dm; 2dm và 1dm; 1dm; 0,5dm

Lời giải:

a. Ta có: 4/8 = 5/10 = 6/12 .Vậy hai tam giác đó đồng dạng

b. Ta có: 3/9 = 6/12 ≠ 4/15 . Vậy hai tam giác đó không đồng dạng.

c. Ta có: 1/2 = 1/2 = 0.5/1 . Vậy hai tam giác đó đồng dạng.

Bài 30 trang 90 sách bài tập Toán 8 Tập 2: Tam giác vuông ABC (∠A = 90^o) có AB = 6cm, AC =8cm và tam giác vuông A’B’C’ (∠A = 90^o) có A’B’ = 9cm, B’C’ = 15cm. Hỏi rằng hai tam giác vuông ABC và A’B’C’ có đồng dạng với nhau không? Vì sao?

Lời giải:

* Trong tam giác vuông A’B’C’ có ∠A = 90^o

Áp dụng định lí Pi-ta-go, ta có: A’B’² + A’C’² = B’C’²

Suy ra: A’C’² = B’C’² - A’B’² = 15² - 9² = 144

Suy ra: A’C’ = 12 (cm)

* Trong tam giác vuông ABC có ∠A = 90^o

Áp dụng định lí Pi-ta-go, ta có: BC² = AB² + AC² = 6² + 8² =100

Suy ra: BC = 10 (cm)

Ta có:

Suy ra:

Vậy ΔA’B’C’ đồng dạng ΔABC (c.c.c)

Bài 31 trang 90 sách bài tập Toán 8 Tập 2: Tam giác ABC có ba đường trung tuyến cắt nhau tại O. Gọi P,Q, R theo thứ tự là trung điểm của các đoạn thẳng OA, OB, OC. Chứng minh rằng tam giác PQR đồng dạng với tam giác ABC

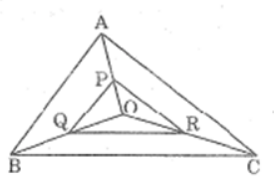
Lời giải:

Trong ΔOAB, ta có PQ là đường trung bình nên: PQ =1/2 AB (tính chất đường trung bình của tam giác)

Suy ra: 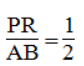(1)

Trong ΔOAC, ta có PR là đường trung bình nên:

PR = 1/2 AC (tính chất đường trung bình của tam giác)

Suy ra: 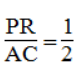(2)

Trong ΔOBC, ta có QR là đường trung bình nên

QR = 1/2 BC (tính chất đường trung bình của tam giác)

Suy ra:

Từ (1), (2) và (3) suy ra:

Vậy ΔPQR đồng dạng ΔABC (c.c.c)