(SGK + SBT) Giải Toán 8 trang 13 Kết nối tri thức, Chân trời sáng tạo, Cánh diều
Haylamdo giới thiệu lời giải bài tập Toán 8 trang 13 Kết nối tri thức, Chân trời sáng tạo, Cánh diều sẽ giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 trang 13.
(SGK + SBT) Giải Toán 8 trang 13 Kết nối tri thức, Chân trời sáng tạo, Cánh diều
- Toán lớp 8 trang 13 Tập 1 (sách mới):
- Toán lớp 8 trang 13 Tập 2 (sách mới):
Lưu trữ: Giải SBT Toán 8 trang 13 (sách cũ)
Bài 48 trang 13 SBT Toán 8 Tập 1: Làm tính chia:
a. (6x2 + 13x – 5) : (2x + 5)
b. (x3 – 3x2 + x – 3) : (x – 3)
c. (2x4 + x3 – 5x2 – 3x – 3) : (x2 – 3)
Lời giải:
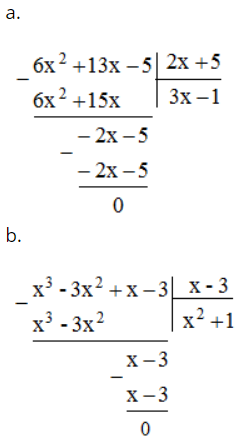
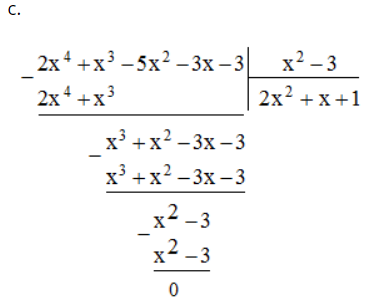
Bài 49 trang 13 SBT Toán 8 Tập 1: Sắp xếp các đa thức sau theo lũy thừa giảm của biến rồi thực hiện phép chia:
a. (12x2 – 14x + 3 – 6x3 + x4) : (1 – 4x + x2)
b. (x5 – x2 – 3x4 + 3x + 5x3 – 5) : (x2 – 3x + 5)
c. (2x2 – 5x3 + 2x + 2x4 – 1) : (x2 – x – 1)
Lời giải:
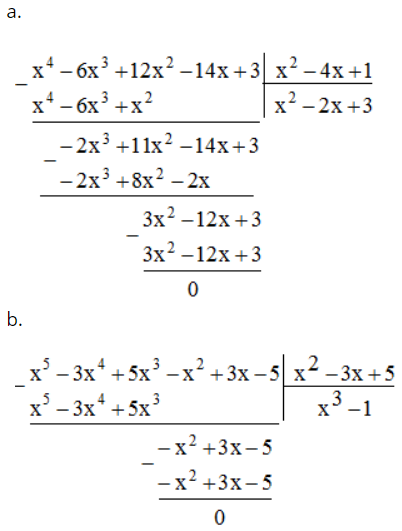
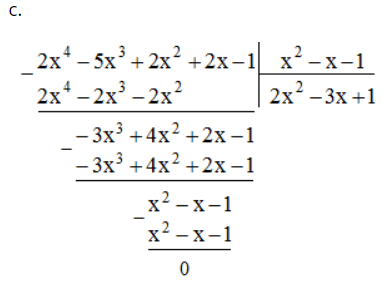
Bài 50 trang 13 SBT Toán 8 Tập 1: Cho hai đa thức A = x4 – 2x3 + x2 + 13x -11 và B = x2 – 2x + 3. Tìm thương Q và số dư R sao cho A = B.Q + R.
Lời giải:
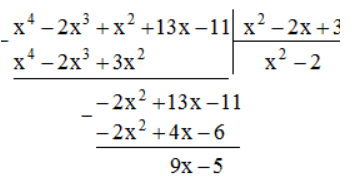
Thương Q = x2 – 2
Dư R = 9x – 5
Vậy x4 – 2x3 + x2 + 13x - 11 = (x2 – 2x + 3)( x2 – 2) + (9x – 5)
Bài 51 trang 13 SBT Toán 8 Tập 1: Tìm a để đa thức x4 – x3 + 6x2 - x + a chia hết cho đa thức x2 – x + 5
Lời giải:
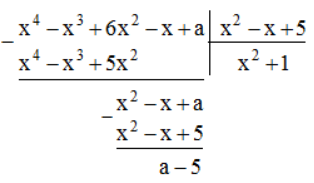
Để có phép chia hết thì số dư phải bằng 0.
Ta có: a – 5 = 0 hay a = 5.
Bài 52 trang 13 SBT Toán 8 Tập 1: Tìm giá trị nguyên của n để giá trị biểu thức 3n3 + 10n2 – 5 chia hết cho giá trị của biểu thức 3n + 1.
Lời giải:
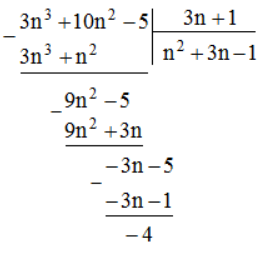
Ta có: 3n3 + 10n2 – 5 = (3n + 1)(n2 + 3n – 1) – 4
Để phép chia đó là chia hết thì 4 ⋮ 3n + 1=> 3n + 1 ∈ Ư(4)
3n + 1 ∈ {-4; -2; -1; 1; 2; 4}
3n + 1 = -4=> 3n = -5=> n = ∉ Z : loại
3n + 1 = -2=> 3n = -3=> n = -1
3n + 1 = -1=> 3n = -2=> n = ∉ Z : loại
3n + 1 = 1=> 3n = 0=> n = 0
3n + 1 = 2=> 3n = 2=> n = ∉ Z : loại
3n + 1 = 4=> 3n = 3=> n = 1
Vậy n ∈ {-1; 0; 1} thì 3n3 + 10n2 – 5 chia hết cho 3n + 1.

