Bài 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61 trang 15 SBT Toán 8 tập 2

---

Bài 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61 trang 15 SBT Toán 8 tập 2

Bài 51 trang 15 sách bài tập Toán 8 Tập 2: Trong một buổi lao động, lớp 8A gồm 40 học sinh chia thành hai tốp: tốp thứ nhất trồng cây và tốp thứ hai làm vệ sinh. Tốp trồng cây đông hơn tốp làm vệ sinh là 8 người. Hỏi tốp trồng cây có bao nhiêu học sinh?

Lời giải:

Gọi x là số học sinh tốp trồng cây. Điểu kiện: x ∈ N*, 8 < x < 40

Số học sinh thuộc tốp làm vệ sinh là x - 8

Tổng số học sinh toàn lớp là 40 nên ta có phương trình:

x + (x – 8) = 40

⇔ x + x = 40 + 8

⇔ 2x = 48

⇔ x = 24 (thỏa)

Vậy số học sinh thuộc tốp trồng cây là 24 (học sinh).

Bài 52 trang 15 sách bài tập Toán 8 Tập 2: Ông của Bình hơn Bình 58 tuổi. Nếu cộng tuổi của bổ Bình và hai lẩn tuổi của Bình thì bằng tuổi của ông và tổng số tuổi của ba người bằng 130. Hãy tính tuổi của Bình.

Lời giải:

Gọi x là số tuổi của Bình. Điều kiện: x ∈N*.

Số tuổi của ông Bình là x + 58.

Cộng tuổi của bố Bình và hai lần tuổi của Bình thì bằng tuổi của ông nên ta có:

(x + 58) - 2x = 58 - x

Số tuổi của ba người bằng 130 nên ta có:

x + (x + 58) + (58 – x) = 130

⇒ x + x + 58 + 58 – x = 130

⇒ x = 130 – 58 – 58

⇒ x = 14 (thỏa)

Vậy Bình 14 tuổi.

Bài 53 trang 15 sách bài tập Toán 8 Tập 2: Một số tự nhiên lẻ có hai chữ số và chia hết cho 5. Hiệu của hai số đó và chữ số hàng chục của nó bằng 68. Tìm số đó.

Lời giải:

Gọi x là chữ số hàng chục. Điều kiện: x ∈N*, 0 < x ≤ 9.

Số tự nhiên lẻ có hai chữ số và chia hết cho 5 có dạng: (*5)= 10x + 5

Vì hiệu của số đó và chữ số hàng chục bằng 68 nên ta có phương trình:

(10x + 5) – x = 68

⇔ 10x + 5 – x = 68

⇔ 10x – x = 68 – 5

⇔ 9x = 63

⇔ x = 7 (thỏa)

Vậy số cần tìm là 7 + 68 = 75.

Bài 54 trang 15 sách bài tập Toán 8 Tập 2: Một phân số có tử số bé hơn mẫu số là 11. Nếu tăng tử số lên 3 đơn vị và giarm mẫu số đi 4 đơn vị thì được một phân số bằng 3/4 .Tìm phân số ban đầu.

Lời giải:

Gọi x là tử số. Điểu kiện: x ∈Z, x ≠ -11 và x ≠ -7

Mẫu số là x + 11.

Tử số tăng thêm 3: x + 3

Mẫu số giảm đi 4: (x + 11) – 4 = x + 7

Phân số mới bằng 3/4 nên ta có phương trình:

(x + 3)/(x + 7) = 3/4

⇔ 4(x + 3) = 3(x + 7)

⇔ 4x + 12 = 3x + 21

⇔ 4x – 3x = 21 – 12

⇔ x = 9 (thỏa)

Tử số là 9, mẫu đô là 9 + 11 = 20

Vậy phân số đã cho là 9/20 .

Bài 55 trang 15 sách bài tập Toán 8 Tập 2: Một số thập phân có phần nguyên là số có một chữ số. Nếu viết thêm chữ số 2 vào bên trái số đó, sau đó chuyển dấu phẩy sang trái một chữ số thì được số mới bằng 9/10 số ban đầu. Tìm số thập phân ban đầu.

Lời giải:

Gọi x là số cần tìm. Điều kiện x > 0

Vì phần nguyên là một số có một chữ số nên khi viết số 2 vào bên trái thì số đó tăng thêm 20 đơn vị.

Giá trị số mới là 20 + x.

Vì chuyển dấu phẩy sang trái một chữ số thì số đó giảm đi 10 lần nên khi chuyển dấu phẩy sang trái một chữ số đối với số 20 + x thì nó có giá trị là (20 + x)/10 .

Số mới bằng 9/10 số ban đầu nên ta có phương trình:

(20 + x)/10 = 9/10 x

⇔ 20 + x = 9x

⇔ 9x – x = 20

⇔ 8x = 20

⇔ x = 2,5 (thỏa)

Vậy số cần tìm là 2,5.

Bài 56 trang 15 sách bài tập Toán 8 Tập 2: Một ô tô đi từ Hà Nội lúc 8 giờ sáng, dự kiến đến Hải Phòng vào lúc 10 giờ 80 phút. Nhưng mỗi giờ ô tô đã đi chậm hơn so với dự kiến là 10km nên mãi đến 11 giờ 20 phút xe mới tới Hải Phòng. Tính quãng đường Hà Nội - Hải Phòng.

Lời giải:

Gọi x (km) là quãng đường Hà Nội - Hải Phòng. Điều kiện: x < 0

Thời gian dự định đi:

10 giờ 30 phút - 8 giờ = 2 giờ 30 phút = 5/2 giờ

Thời gian thực tế đi:

11 giờ 20 phút - 8 giờ = 3 giờ 20 phút = 10/3 giờ

Vận tốc dự định đi: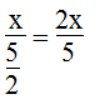(km/h)

Vận tốc thực tế đi: 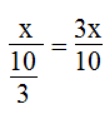(km/h)

Vận tốc thực tế đi chậm hơn vận tộc dự định đi 10 km/h nên ta có phương trình:

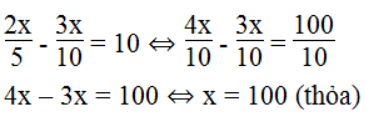
Vậy quãng đường Hà Nội - Hải Phòng dài 100km.

Bài 57 trang 15 sách bài tập Toán 8 Tập 2: Một tàu chở hàng từ ga Vinh về ga Hà Nội. Sau đó 1,5 giờ, một tàu khách xuất phát từ ga Hà Nội đi Vinh với vận tốc lớn hơn vận tốc tàu chở hàng là 7km/h. Khi tàu khách đi được 4 giờ thì nó còn cách tàu hàng là 25km. Tính vận tốc mỗi tàu, biết rằng hai ga cách nhau 319km.

Lời giải:

Gọi x (km/h) là vận tốc của tàu hàng. Điều kiện: x > 0

Vận tốc của tàu khách là x + 7 (km/h)

Thời gian tàu hàng từ lúc đi đến lúc cách tàu khách 25km là:

1,5 + 4 = 5,5 (giờ)

Quảng đường tàu hàng di được trong 5,5 giờ là 5,5x (km)

Quãng dường tàu khách đi được trong 4 giờ là 4(x + 7) (km)

Theo đề bài ta có phương trình:

5,5x + 4(x + 7) = 319 - 25 ⇔ 5,5x + 4x + 28 = 294

⇔ 9,5x = 294 - 28 ⇔ 9,5x = 266 ⇔ x = 28 (thỏa)

Vậy vận tốc của tàu hàng là 28 km/h.

Vận tốc của tàu khách là 28 + 7 = 85 km/h.

Bài 58 trang 15 sách bài tập Toán 8 Tập 2: Một người đi xe đạp từ A đến B. Lúc đầu, trên đoạn đường đá, người đó đi với vận tốc 10km/h. Trên đoạn đường còn lại là đường nhựa, dài gấp rưỡi đoạn đường đá, người đó đi với vận tốc 15km/h. Sau 4 giờ, người đó đến B. Tính độ dài đoạn đường AB.

Lời giải:

Gọi x (km) là quãng đường đá. Điểu kiện: x > 0.

Chiều dài đoạn đường nhựa là 1,5x (km).

Thời gian đi đoạn đường đá là x/10 (giờ)

Thời gian đi đoạn đường nhựa là (1,5x)/15 (giờ).

Sau 4 giờ người đó đến B nên ta có phương trình:

x/10 + (1,5x)/15 = 4 ⇔ 3x/30 + 3x/30 = 120/30

⇔ 3x + 3x = 120 ⇔ 6x = 120 ⇔ x = 20 (thỏa)

Đoạn đường đá dài 20km, đoạn đường nhựa dài 20.1,5 = 30km.

Vậy quãng đường AB dài 20 + 30 = 50km.

Bài 59 trang 15 sách bài tập Toán 8 Tập 2: Bánh trước của máy kéo có chu vi là 2,5m, bánh sau có chu vi là 4m. Khi máy kéo đỉ từ A. đến B, bánh trước quay nhiều hơn bánh sau 15 vòng. Tính khoảng cách AB.

Lời giải:

Gọi x (m) là khoảng cách từ A đến B. Đỉều kiện: x > 0

Khi đi hết đoạn đường từ A đến B, số vòng quay của bánh xe trước là x/(2,5) (vòng), số vòng quay của bánh xe sau là x/4 (vòng)

Vì bánh xe trước quay nhiều hơn bánh xe sau 15 vòng nên ta có phương trình:

x/(2,5) - x/4 = 15

⇔ 8x/20 - 5x/20 = 300/20

⇔ 8x – 5x = 300

⇔ 3x = 300

⇔ x = 100 (thỏa)

Vậy A cách B 100m.

Bài 60 trang 15 sách bài tập Toán 8 Tập 2: Một miếng hợp kim đống và thiếc có khối lượng là 12kg, chứa 45% đồng. Hỏi phải thêm vào đó bao nhiêu thiếc nguyên chất để được hợp kim mới có chứa 40% đồng.

Lời giải:

Gọi x (kg) là khối lượng thiếc thêm vào. Điều kiện: x > 0.

Khối lựợng miếng hợp kim sau khi thêm là x + 12 (kg).

Khối lượng đồng có trong 12kg hợp kim chứa 45% đồng là:

12.45/100 = 5,4 (kg)

Vì khối lượng đồng không đổi trong hợp kim mới chứa 40% đồng nên ta có phương trình:

(5,4)/x + 12 = 40/100

⇔ (5,4)/x + 12 = 4/10

⇔ 5,4.10 = 4(x + 12)

⇔ 54 = 4x + 48

⇔ 4x = 54 – 48

⇔ 4x = 6

⇔ x = 1,5 (thỏa)

Vậy phải thêm vào l,5kg thiếc.

Bài 61 trang 15 sách bài tập Toán 8 Tập 2: Một cửa hàng bản một máy vi tỉnh với giá 6,5 triệu đồng chưa kể thuế giá trị gia tăng (VAT). Anh Trọng mua máy vi tính đó cùng với một môđem ngoài và phải trả tổng cộng là 7,546 triệu đồng, trong đó đã tính cả 10% thuế VAT. Hỏi tiền mua chiếc môđem (không kể VAT) là bao nhiêu?

Lời giải:

Gọi x (triệu đồng) là số tiền mua môđem chưa kể thuế VAT. Điều kiện: x > 0

Số tiền mua máy tính và môđem chưa kế thuế VAT:

6,5 + x (triệu đồng)

Số tiền thuế VAT phải trả là: (6,5 + x).10% (triệu đồng)

Tổng số tiền anh Trọng phải trả là 7,546 triệu đồng nên ta có phương trình:

(6,5 + x) + (6,5 + x).10% = 7,546

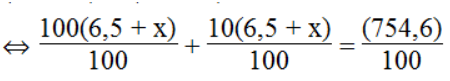
⇔ 100(6,5 + x) + 10(6,5 + x) = 754,6

⇔ 650 + 100x + 65 + 10x = 754,6

⇔ 100x + 10x = 754,6 – 650 – 65

⇔ 110x = 39,6 ⇔ x = 0,36 (thỏa)

Vậy giá của môđem là 0,36 triệu đồng = 360.000 đồng.