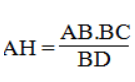(SGK + SBT) Giải Toán 8 trang 97 Kết nối tri thức, Chân trời sáng tạo, Cánh diều

---

Haylamdo giới thiệu lời giải bài tập Toán 8 trang 97 Kết nối tri thức, Chân trời sáng tạo, Cánh diều sẽ giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 trang 97.

(SGK + SBT) Giải Toán 8 trang 97 Kết nối tri thức, Chân trời sáng tạo, Cánh diều

- Toán lớp 8 trang 97 Tập 1 (sách mới):

• Giải Toán 8 trang 97 Chân trời sáng tạo

  Xem lời giải

• Giải Toán 8 trang 97 Cánh diều

  Xem lời giải

• Giải Toán 8 trang 97 Kết nối tri thức

  Xem lời giải

- Toán lớp 8 trang 97 Tập 2 (sách mới):

---

---

---

Lưu trữ: Giải SBT Toán 8 trang 97 (sách cũ)

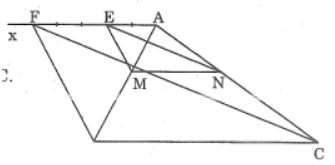
Bài 51 trang 97 sách bài tập Toán 8 Tập 2: Cho tam giác ABC.

a. Trên cạnh AB lấy điểm M sao cho AM/MB = 2/3 tìm trên AC điểm N sao cho AN/NC = 2/3

b. Vẽ đoạn thẳng MN.Hỏi rằng hai đường thẳng MN và BC có song song với nhau không? Vì sao?

c. Cho biết chu vi và diện tích của tam giác ABC thứ tư là P và S.

Tính chu vi và diện tích tam giác AMN.

Lời giải:

* Cách vẽ:

- Kẻ tỉa AX bất kỉ khác tia AB, AC

- Trên tỉa Ax, lấy hai điểm E và F sao cho AE = 2(đvd), EF = 3(đvd)

- Kẻ đường thẳng FB

- Từ E kẻ đường thẳng song song với FB Cắt AB tại M.

- Kẻ đường thẳng FC.

- Từ E kẻ đường thẳng song song với FC cắt AC tại N.

Ta có M, N là hai điểm cần vẽ.

* Chứng minh:

Trong ΔAFB, ta có: EM /FB.

Theo định lí Ta-lét, ta có:

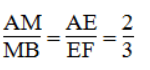
Trong ΔAFC, ta có: EN // FC.

Theo định lí ta-lét ta có:

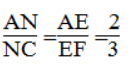
Vậy M, N là hai điểm cần tìm.

b. Trong ΔABC, ta có:

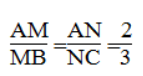
Suy ra: MN // BC (Theo định lí đảo của định lí Ta-lét)

c. Gọi p' và S' là chu vi và diện tích của ΔAMN.

Trong ΔABC, ta có: MN // BC

Suy ra: ΔAMN đồng dạng ΔABC

Theo tính chất hai tam giác đồng dạng ta có:

p'p = 2/3 = k ⇒ p'.= 2/3 p

S'S = ( 2/3 )² = 4/9 = k² ⇒ S' = 4/9 S

Bài 52 trang 97 sách bài tập Toán 8 Tập 2: Tứ giác ABCD có hai góc vuông tại đỉnh A và C hai đường chéo AC và BD cắt nhau tại O ,(BAO) = (BDC) .Chứng minh:

a.ΔABO đồng dạng ΔDCO

b. ΔBOC đồng dạng ΔADO

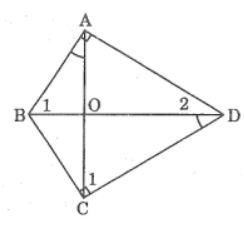
Lời giải:

Xét ΔABO và ΔDCO,ta có:

∠(BAO) = ∠(BDC) (gt)

Hay ∠(BAO) = ∠(ODC)

∠(AOB) = ∠(DOC) (đối đỉnh)

Vậy ΔABO đồng dạng ΔDCO (g.g)

b, Vì ΔABO đồng dạng ΔDCO nên:

∠(B₁ ) = ∠(C₁ ) (1)

Mà ∠(C₁ ) + ∠(C₂ ) = ∠(BCD) = 90^o (2)

Trong ΔABD, ta có: ∠A = 90^o

Suy ra: ∠(B₁ ) + ∠(D₂ ) = 90^o (3)

Từ (1), (2) và (3): Suy ra: ∠(C₂ ) = ∠(D₂ )

Xét ΔBCO và ΔADO, ta có:

∠(C₂ ) = ∠(D₂ ) (chứng minh trên)

∠(BOC) = ∠(AOD) (đối đỉnh)

Vậy ΔBOC đồng dạng ΔADO (g.g).

Bài 53 trang 97 sách bài tập Toán 8 Tập 2: Cho hình chữ nhật ABCD có AB = a = 12cm, BG = b = 9m. Gọi H là chân đường vuông góc kẻ từ A xuống BD

a. Chứng minh ΔAHB đồng dạng ΔBCD

b. Tính độ dài đoạn thắng AH

c. Tính diện tích tam giác AHB.

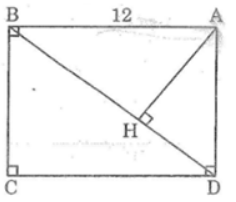
Lời giải:

Xét ΔAHB và. ΔBCD, ta có:

∠(AHB) = ∠(BCD) =90^o

AB // CD (gt)

∠(ABH) = ∠(BDC) (so le trong)

Vậy ΔAHB đồng dạng ΔBCD (g.g)

Vì ΔAHB đồng dạng ΔBCD nên:

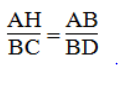
Suy ra:

Áp dụng định lí Pi-ta-go vào tam giác vuông BCD,ta có:

BD² = BC² + CD² = BC² + AB²

= 12² + 9² = 225

Suy ra: BD = 15cm

Vậy AH = (12.9)/15 = 7,2 cm

Vì ΔAHB đồng dạng ΔBCD nên 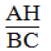= (7.2)/9 = 0,8

Ta có: 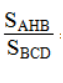= k² = (0,8)² = 0,64 ⇒ S_AHB = 0,64S_BCD

S_BCD = 1/2 BC.CD = 1/2 .12.9 = 54(cm²)

Vậy S_AHB = 0,64.S_BCD = 0,64.54 = 34,56 (cm²).

Bài 54 trang 97 sách bài tập Toán 8 Tập 2: Tứ giác ABCD có hai dường chéo AC và BD cắt nhau tại O, ∠(ABD) = ∠(ACD) . Gọi E là giao điểm của hai đường thẳng AD và BC. Chứng minh rằng:

a. ΔAOB đồng dạng ΔDOC

b. ΔẠOD đồng dạng ΔBOC

c. EA.ED = EB.EC.

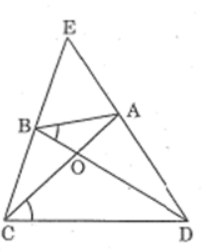
Lời giải:

Xét ΔAOB và ΔDOC, ta có:

∠(ABD) = ∠(ACD) (gt)

Hay ∠(ABO) = ∠(OCD)

∠(AOB) = ∠(DOC) (đối đỉnh)

Vậy ΔAOB đồng dạng ΔDOC (g.g)

Vì ΔAOB đồng dạng ΔDOC nên:

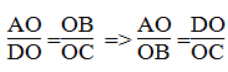
Xét ΔAOD và BOC ta có:

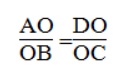
∠(AOD) = ∠(BOC) (đối đỉnh)

Vậy ΔAOD đồng dạng ΔBOC (c.g.c)

Vì ΔAOD đồng dạng ΔBOC nên: ∠(ADC) = ∠(BCO) hay ∠(EDB) = ∠(ECA)

Xét ΔEDB và ΔECA ta có:

∠E chung

∠(EDB) = ∠(ECA) (chứng minh trên)

Vậy ΔEDB đồng dạng ΔECA(g.g)

Suy ra:

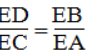
⇒ ED.EA = EC.EB